【 問 題 １ 】

次の４次方程式を解け
　　x⁴＋x³＋x²＋x ＝ 0

【 解 答 】

明らかに x ＝ 0, −1　だから、問題の式は次のように表すことができる。
　　x ( x＋1 )( x²＋ax＋b ) ＝ 0
したがって、
　　x⁴＋( a＋1 ) x³＋( a＋b ) x²＋bx ＝ 0
これと問題の式とを比べて、
　　a ＝ 0 ,　b ＝ 1
したがって、
　　x ( x＋1 )( x²＋1 ) ＝ 0
よって、
　　x ( x＋1 )( x＋i )( x−i ) ＝ 0
したがって、答えは、
　　x ＝ 0, −1,　i, −i

【 問 題 ２ 】

次の４次方程式を解け
　　x⁴＋x³＋x²＋x ＝ −1

【 解 答 】

x⁴＋x³＋x²＋x＋1 ＝ 0
明らかに x ≠ 0




　　
　　





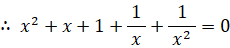
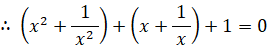
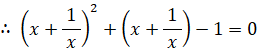
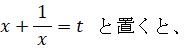
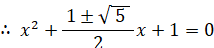
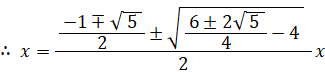
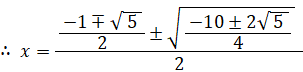
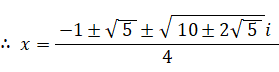
つまり、４次方程式の解は次の４つである。
　　
　　
　　
　　

【 別 解 その１ ( ラグランジュの方法 ) 】

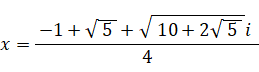
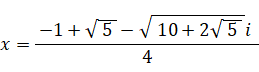
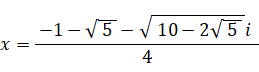
明らかに x ≠ 1
x⁴＋x³＋x²＋x＋1 ＝ 0　の両辺に ( x−1 ) をかけると、
　　x⁵−1 ＝ 0
ということは、x⁴＋x³＋x²＋x＋1 ＝ 0　の解は 1 以外の５乗すると 1 になる複素数である。
それらを、ε¹, ε², ε³, ε⁴ と置くと、
　　　ε¹ ＝ a ＋ b i
　　　ε² ＝ c ＋ d i
　　　ε³ ＝ c − d i
　　　ε⁴ ＝ a − b i
　　　1 ＋ ε¹ ＋ ε² ＋ ε³ ＋ ε⁴ ＝ 0
　　　ε¹ ＋ ε⁴ ＝ 2a
　　　ε² ＋ ε³ ＝ 2c
　　　ε¹ × ε⁴ ＝ 1
　　　ε² × ε³ ＝ 1

( x−ε¹ ) ( x−ε² ) ( x−ε³ ) ( x−ε⁴ ) ＝ 0
∴　{ ( x−ε¹ ) ( x−ε⁴ ) } { ( x−ε² ) ( x−ε³ ) }　＝　0
∴　{ x² − ( ε¹ ＋ ε⁴ ) x ＋ ε¹×ε⁴ } { x² − ( ε² ＋ ε³ ) x ＋ ε²×ε³ }　＝　0
∴　( x² − 2a x ＋ 1 ) ( x² − 2c x ＋ 1 )　＝　0
x ≠ 0 なので、この式は次のように変形することができる。
　　
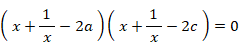
ここで、次のように置く。
　　
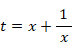
すると、次のようになる。
　　
よって、次のようになる。
　　t ＝ 2a,　2c
　　t ² − ( 2a＋2c ) t ＋ 4ac ＝ 0
　　∴　t ² − ( ε¹＋ε²＋ε³＋ε⁴ ) t + ( ε¹＋ε⁴ ) ( ε²＋ε³ ) ＝ 0
　　∴　t ² − ( ε¹＋ε²＋ε³＋ε⁴ ) t + ( ε³＋ε⁴＋ε¹＋ε² ) ＝ 0
　　∴　t ² ＋ t − 1 ＝ 0
　　
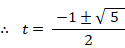
したがって、次のようになる。
　　
　　
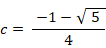
したがって、
　　
　　　　　　　　
　　　　　　　　
　　
　　　　　　　　
　　　　　　　　
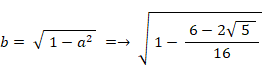
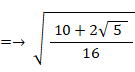
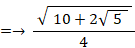
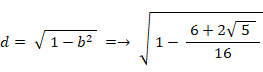
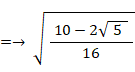
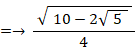
というわけで、４次方程式の解は次の４つになる。
　　
　　
　　
　　

【 別 解 その２ 】

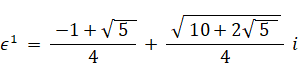
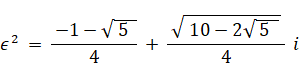
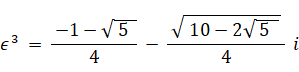
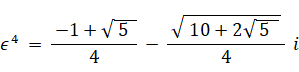
明らかに x ≠ 1
x⁴＋x³＋x²＋x＋1 ＝ 0　の両辺に ( x−1 ) をかけると、
　　x⁵−1 ＝ 0
ということは、x⁴＋x³＋x²＋x＋1 ＝ 0　の解は 1 以外の５乗すると 1 になる複素数である。
あとは、数理論 ＞ １の５乗根の複素平面 をご覧ください。