【 問 題 】
-
一辺の長さが 1 の正方形がある。点P は辺CD上を自由に移動し、点Q は辺BC上を自由に移動する。
今、∠QAP = 45° という条件を付けて、点P と 点Q を連動させた。
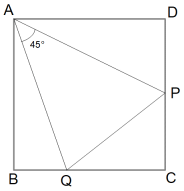
(1) DPの長さを x 、BQの長さを y として、y を x の式で表せ。
(2) tan 22.5° の値を求めよ。
(1)
-
PQ の長さを2通りの方法で表すことから始めます。
まずはピタゴラスの定理より、
(PQ)2 = (1−x) 2 + (1−y) 2 =→ x 2 + y 2 − 2(x+y) + 2
△APD を点Aを中心に回転させて、辺AD を 辺AB に重ねる。すると、点P は 点P' に移動する。
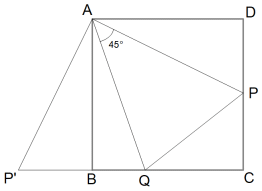
△AP'Q と △APQ は合同である。
したがって、 PQ = x+y
以上より、次の式が成り立ちます。
(x+y)2 = x 2 + y 2 − 2(x+y) + 2
よって、
x 2 + y 2 + 2xy = x 2 + y 2 − 2(x+y) + 2
よって、
2xy = −2(x+y) + 2
よって、
y(1+x) = 1−x
よって、
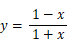
-
∠PAD = 22.5° のとき y = x だから
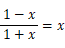
よって、
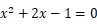
0 ≦ x ≦ 1 の範囲で上の式を解くと、
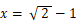
よって、
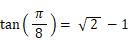
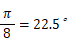
 幾何学 へ戻る
幾何学 へ戻る