(4) 変速度運動にまつわる 出題頻度の多い問題たち
-
問題

質量
 の物質が、 速さ
の物質が、 速さ  で半径
で半径  の等速円運動をしています。 このとき、 円の中心に向かって働いている向心力
の等速円運動をしています。 このとき、 円の中心に向かって働いている向心力  はいくらでしょうか?
はいくらでしょうか?ヒント : ニュートンの運動方程式を使います。
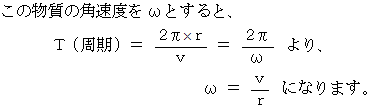
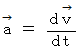 です。
です。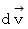 は、 大きさが、 中心角
は、 大きさが、 中心角 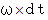 , 半径
, 半径  の円弧の長さにほぼ等しく、
の円弧の長さにほぼ等しく、円の中心を向いています。
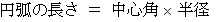 です。
です。答え :
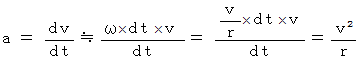
したがって、
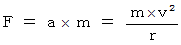
または、
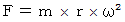
問題

-
静止している振り子の重りの先端は必ず地球の重力と遠心力との合力の方向を向いています。 さて、 緯度(
 度 )にある振り子の 質量(
度 )にある振り子の 質量( 
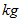 ) の重りに働く地球の自転による遠心力(
) の重りに働く地球の自転による遠心力( 
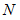 ) を求めなさい。 ただし、 地球の赤道半径(
) を求めなさい。 ただし、 地球の赤道半径( 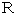 )を
)を 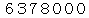
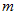 とします。
とします。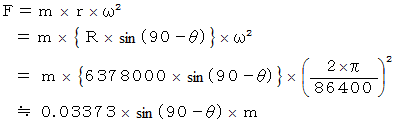
遠心力は赤道上が最大で
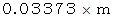
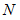 になります。
になります。重力は
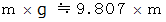
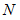 ですから、 赤道上でも遠心力は重力の
ですから、 赤道上でも遠心力は重力の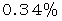 くらいしかありません。
くらいしかありません。
-
糸の長さが
 , おもりの質量が
, おもりの質量が  の単振り子が、 鉛直下方向に対して
の単振り子が、 鉛直下方向に対して  の角度をなす位置から静かに離されて振動するとき、 おもりの最高スピードはいくらになるでしょうか?
の角度をなす位置から静かに離されて振動するとき、 おもりの最高スピードはいくらになるでしょうか?ただし、 重力変速度を
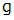 とします。
とします。ヒント : 最高速度に達するのは、 おもりが最下点を通過する時です。 力学的エネル
ギー保存の法則を用いて解答を導いてください。
答え : 力学的エネルギー保存の法則より、 おもりのエネルギーは次のようになります。
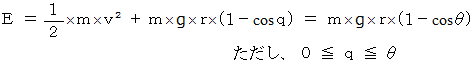
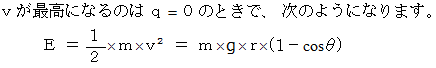
これを
 について解くと、 次のようになります。
について解くと、 次のようになります。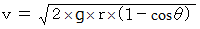

-
上記の単振り子の周期は、
 や
や  に関係なく、 次の式で表されることを示しなさい。
に関係なく、 次の式で表されることを示しなさい。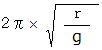
答え : 私には難しすぎるので、 只今勉強中です。

-
初速
 , 角度
, 角度  で投げ出された砲丸は、 最高の高さ
で投げ出された砲丸は、 最高の高さ 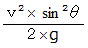 まで達し、 時間
まで達し、 時間 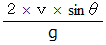 の後に、
の後に、 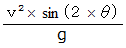 の距離先に落下する。 したがって、 初速
の距離先に落下する。 したがって、 初速  が一定の時、 砲丸投げの記録が最高になるのは、
が一定の時、 砲丸投げの記録が最高になるのは、 -
砲丸は、 垂直方向には、 初速
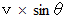 , 加速度
, 加速度 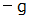 の等加速度運動を行い、水平方向には、速さ
の等加速度運動を行い、水平方向には、速さ 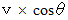 の等速直線運動を行う。
の等速直線運動を行う。● 砲丸の到達する最高の高さの求め方 :
-
砲丸が時間
 の後に、 最高の高さに達するとすると、 垂直方向の砲丸の速さは、 初速が
の後に、 最高の高さに達するとすると、 垂直方向の砲丸の速さは、 初速が 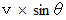 で、 傾き
で、 傾き 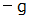 で減っていき、 時間
で減っていき、 時間  の後に
の後に  になる。 速さの増加分を時間で割れば、 加速度になるので、 次の式が成り立つ。
になる。 速さの増加分を時間で割れば、 加速度になるので、 次の式が成り立つ。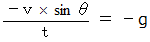
この間に砲丸が移動した垂直方向の距離は、 垂直方向の砲丸の速さを時間で積分することにより得られる。 横軸に時間、 縦軸に垂直方向の砲丸の速さをとり、 時間を

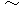
 の間でグラフを作ると、 横軸 と 縦軸 と グラフの直線 によって直角三角形ができるが、 この直角三角形の面積が、 砲丸の垂直方向の速さを時間で積分したものを表しているので、 次の式になる。
の間でグラフを作ると、 横軸 と 縦軸 と グラフの直線 によって直角三角形ができるが、 この直角三角形の面積が、 砲丸の垂直方向の速さを時間で積分したものを表しているので、 次の式になる。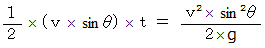
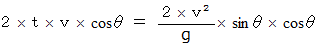
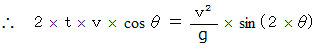
 次のページへ進む
次のページへ進む