(1) 減速運動も加速度運動に含まれる。
-
私は、「 加速度 」という言いかたを「 変速度 」に変えたほうが、 誤解がなくていいのではないかと考えています。 なぜなら、「 加速度運動 」とは、 速度が加わる運動だけではないからです。 速度が変化する運動はすべて「 加速度運動 」だからです。 減速する場合も「 加速度運動 」なのです。
速度 : 微小経過時間あたりの移動空間( 移動空間は、距離と方向を持つ。)
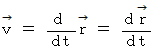
速度の大きさ : 微小時間経過直前の位置 から 微小時間経過直後の位置 までの距離
を微小時間で割ったもの
速度の方向 : 微小時間経過直後の位置 の 微小時間経過直前の位置 に対する方向
変速度 : 微小経過時間あたりの速度の変化( 速度の変化は、大きさと方向を持つ。)

変速度の大きさ : 微小時間経過直後の速度 から 微小時間経過直前の速度 を ベクトル的に引くことによって得られるベクトル の大きさ
変速度の方向 : 微小時間経過直後の速度 から 微小時間経過直前の速度 を ベクトル的に引くことによって得られるベクトル の向き
等速度運動 : 変速度 = 0 いわゆる、 等速直線運動のことである。
等変速度運動 : 変速直線運動である。 速度の向きと変速度の向きが同じ場合は、 等加速度直線運動。 速度の向きと変速度の向きが逆の場合は、 速度が0になるまでは等減速度直線運動で、 その後は等加速度直線運動。
等速円運動 : 変速度の大きさは一定であるが、 変速度の向きが変化しているので、 等変速度運動ではない。 変速度の向きは、 速度の向きと直角で、 円の中心を向いている。 この加速度の原因となる中心向きの力を向心力という。
単振り子運動 : 変速度の大きさは変化する。 変速度の向きは、 速度の向きと直角で、 振り子の支点を向いている。 この加速度の原因となる中心向きの力を向心力という。
実際に重りに働くのは、 重りの重力の運動方向成分であるが、 重りの運動が紐によって拘束されているため、 それに代わって向心力が作用していると考えるのである。 このとき、 変化する重りの重力の運動方向成分の大きさは、 向心力の大きさを変化させる。
-
単振り子運動では、 重りに作用する重力のひも方向の成分 と ひもの張力 が、 作用反作用の関係でつり合っています。 これは、 支点に対して静止している観察者にとっても、 重りに対して静止している( 支点に対して重りと全く同じ振り子運動をしている )観察者にとっても同じことです。 単振り子の重りが速さ
 で移動している瞬間には、 上記の2つの力以外にも、 次の大きさの向心力が働いています。
で移動している瞬間には、 上記の2つの力以外にも、 次の大きさの向心力が働いています。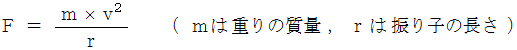
これは、 支点に対して静止している観察者にとっても、 重りに対して静止している観察者にとっても同じことです。 違うのは、 重りに対して静止している観察者にとっては、 向心力と同じ大きさの遠心力が作用していることです。
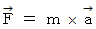 について考える。
について考える。-
ニュートンの運動方程式は、本当ならば
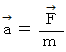 と書くべきではないでしょうか。
と書くべきではないでしょうか。これならば、 原因が右辺で結果が左辺になっていますのでスッキリします。 つまり、
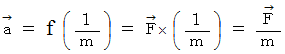
この式の意味は、 変速度の生じやすさを表す
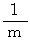 という量を持つ物質に 力
という量を持つ物質に 力  を加えると、 その物質は、 変速度
を加えると、 その物質は、 変速度 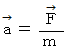 で変速度運動をするということです。
で変速度運動をするということです。しかし、「 相対的力 」とも言うべき「 みかけの力 」というのがあり、 変速度運動をしている観察者からすると、 客観的には何も力は加わっていないのに、 力が作用しているようになります。「 みかけの力 」はその観察者にとっては、 決して幻の力ではなく現実的なものです。 したがって、「 みかけの力 」という言いかたを「 相対的力 」に変えたほうが、 誤解がなくていいのではないかと、 私は思います。 そして、「 相対的力 」については、 次のように書くべきだと思います。
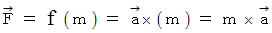
これは、 ニュートンの運動方程式の形そのものです。 ただし、 この式は、 右辺が原因で左辺が結果になっています。 アインシュタインは、「 加速するロケットの中にいる人にとっては、 相対的力 と 重力 とは区別ができない。( 等価原理 ) 変速度運動は力を作る。」といった主旨のことを述べています。
 力学 へ戻る
力学 へ戻る