数理論 へ戻る1000万円の借金をし、 10年後に一括返金するという契約をした。
年間利率 10 % の複利契約である。
10年後の一括返済額は次のようになる。
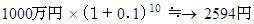
まだ10年後で良かった。 20年後なら 6727万円 だ。
一括返済の時期が遅くなるほどに指数関数的に返済額が増大する仕組みだ。
そこで、 誠意ある金融業者は次のような複利契約を作ってくれた。
それは、 一括返済する時期が遅くなれば年間利率が低くなるというもので、 n 年後の一括返済額は次の式で表される。
n ＝ １ のとき、 借金 × 2
n ＝ ２ のとき、 借金 × 2.25
n ＝ 10 のとき、 およそ 借金 × 2.594
n ＝ 20 のとき、 およそ 借金 × 2.653
n が無限大のとき、 一括返済額はどのようになるだろう？
借金 × ｅ （ ネイピア数 ） ≒→ 借金 × 2.718
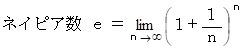
袋の中に n 個の玉が入っている。１個だけ赤色で他はすべて白色である。 袋の中から無作為に１個の玉を取り出して色を確認した後に袋に戻す。 これを n 回繰り返す。 そうしたときに、 赤玉が全く出ない確率は次のようになる。
n ＝ ５ のとき、 約 0.3277
n ＝ 10 のとき、 約 0.3487
n ＝ 100 のとき、 約 0.3660
n が無限大のとき、 赤玉が全く出ない確率はどのようになるだろう？
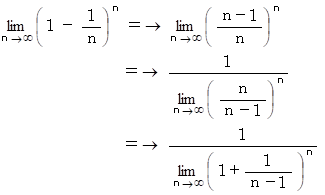
袋の中に n 個の玉が入っている。１個だけ赤色で他はすべて白色である。 袋の中から無作為に１個の玉を取り出して色を確認した後に袋に戻す。 これを n 回繰り返す。 そうしたときに、 赤玉が全く出ない確率を１万回のシミュレーションで見てみよう。