NHK の番組「3か月でマスターする数学」の中で、秋山仁先生が紹介された論理問題です。少し表現方法を変えていますが、次のような問題です。
【 問 題 】
-
佐藤さん夫婦、鈴木さん夫婦、高橋さん夫婦 が 10年ぶりに会うことになりました。待合場所はホテルのロビーです。久しぶりに会った6人は握手を交わします。ただし、みんながみんな握手をしたわけではありません。その後ホテル内の中華レストランでランチとなりました。食事が用意されるまでの会話の中で、高橋の妻さんがみんなに質問しました。「さっき、みんな握手をしていたけど、何人と握手したの?」高橋の夫さんから順番に反時計回りに答えていきます。その結果、高橋の妻さん以外の人はすべて握手をした人の数が異なっていました。では、高橋の妻さんは何人と握手をしていたのでしょうか? もちろん、夫婦どうしは握手をしません。
-
高橋の妻さん以外の人で、握手をした人の数が多い順に並べると、4人だった1人、3人だった1人、2人だった1人、1人だった1人、0人だった1人 になります。
まず、正六角形の頂点になるように6つの ● を描きます。そして時計回りに ● に仮名をつけます。 A → a → B → b → C → c とします。A と a は ある夫婦の夫と妻を表します。次に、A は4人と握手をしたものとして、握手をした相手と線分で結びます。すると、 a は誰とも握手をしなかったことになります。その次に c が3人と握手をしたものとして、握手をした相手と線分で結びます。
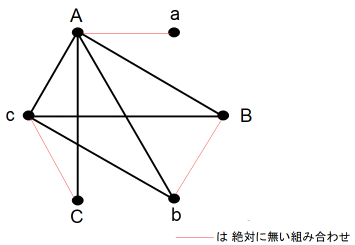
この図では、4人と握手をした1人、3人と握手をした1人、2人と握手をした2人、1人と握手をした1人 となっています。高橋の妻さん以外の人はすべて握手をした人の数が異なっていたのだから、高橋の妻さん( この図では b になる )は2人と握手をしたことが分かります。
以上の図の他に次の3とおりの図を作ってみましたが、どれも高橋の妻さんは2人と握手をしたことになりました。
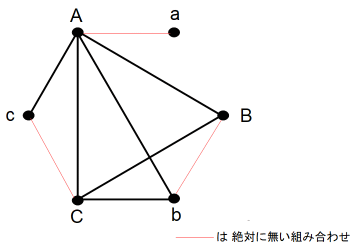
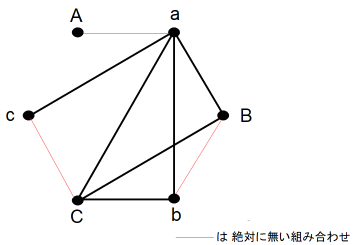
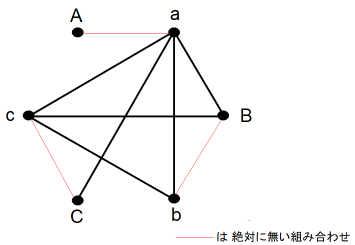
 論理学 へ戻る
論理学 へ戻る