(1)
-
( 問 題 ) 2桁の数で、 4で割ると2余り、 5で割ると3余る数 をすべて述べよ。
( A君の解答 )
4で割ると2余る数 = 4で割ると−2余る数
5で割ると3余る数 = 5で割ると−2余る数
したがって、 求める数は、 4でも5でも割り切れる数から2引いた数である。
したがって、 20n( n は自然数 )から2引いた数である。
よって、 答えは、
18 38 58 78 98
( B君の解答 )
「 4で割ると2余り かつ 5で割り切れる 数 」と「 4で割り切れ かつ 5で割ると3余る 数 」と「 4でも5でも割り切れる数 」とを加えたものは、「 4で割ると2余り かつ 5で割ると3余る 数 」である。
4と5の最小公倍数は20で、 これより小さな数で、「 4で割ると2余り かつ 5で割り切れる 数 」 は 10 であり、「 4で割り切れ かつ 5で割ると3余る 数 」は8である。 したがって、 次の式を満たす2桁の数が答えとなる。
10 + 8 + 20n ( n は0を含む自然数 )
つまり、
18 38 58 78 98
-
( 問 題 ) 3で割ると1余り、 5で割ると3余り、 7で割ると2余る 2桁の正の整数は?
( 解 答 )
ここで登場してくる文字はすべて整数を表すものとする。
3で割ると1余り、 5で割ると3余り、 7で割ると2余る整数を S とすると、





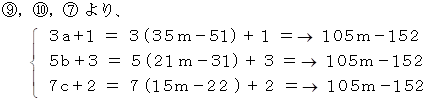
したがって、
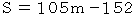
このうち、 2桁の正の整数は、
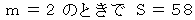
 数理論 へ戻る
数理論 へ戻る