（１） ７で割ると３余り、 かつ、 ９で割ると５余る数

　 ７で割ると３余り、 かつ、 ９で割ると５余る数は、 63の倍数から４を引いた数です。 なぜなのでしょうか？

　 ７で割ると３余り、 かつ、 ９で割ると５余る数は、 ７で割ると−４余り、 かつ、 ９で割ると−４余る数です。 ７で割ると−４余り、 かつ 、 ９で割ると−４余る数から４を引いた数は、 ７でも９でも割り切ることができます。 ７でも９でも割り切ることができる数は、 ７と９の公倍数です。 63は７と９の最小公倍数です。 したがって、 63の倍数から４を引いた数は、 ７で割ると３余り、 かつ、 ９で割ると５余ります。

　　　　　

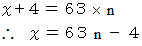
　 以上の表現の方法では、 最後のところが少々理解しづらいのではないかと思います。 そこで、 論理学的な表現に変換してみます。

　 ある数が７で割ると３余り、 かつ、 ９で割ると５余るための必要十分条件は、
その数が７で割ると−４余り、 かつ、 ９で割ると−４余ることです。

　 そのための必要十分条件は、
その数から４を引いた数が、 ７でも９でも割り切ることができることです。

　 そのための必要十分条件は、
その数から４を引いた数が、 ７と９の最小公倍数で割り切ることができることです。

　 そのための必要十分条件は、
その数から４を引いた数が、 63で割り切ることができることです。

　 以上より、 次のことが言えます。
　 ある数が７で割ると３余り、 かつ、 ９で割ると５余るための必要十分条件は、
その数から４を引いた数が、 63で割りきることができることです。

　 ということはつまり、
　 ７で割ると３余り、 かつ、 ９で割ると５余る数は、 63の倍数から４を引いた数であるということです。


　 次の十進BASIC のプログラムは、 ７で割ると３余り、 かつ、 ９で割ると５余る数 をいろんな方法で求めます。

（２） ３で割ると２余り、 かつ、 ５で割ると３余る数

　 ３で割ると２余り、 かつ、 ５で割ると３余る数は、 15の倍数から７を引いた数です。 なぜなのでしょうか？

　 ３で割ると２余る数 に７を加えた数： 3n＋2＋7 ＝→ 3(n＋3）　← ３で割り切れる
　 ５で割ると３余る数 に７を加えた数： 5m＋3＋7 ＝→ 5(m+2)　← ５で割り切れる
　 したがって、３と５の最小公倍数である15の倍数から７を引いた数は、３で割ると２余り、 かつ、 ５で割ると３余る。