【 問 題１ 】

全体集合を 自然数 とする。
ｍ を ｎ で割ると１余るとき、 ｍ^ｋ を ｎ で割ると１余ることを証明せよ。

【 解 答 】

ｍ　＝　ａｎ ＋ １　と置く。
ｍ^２ ＝ （ ａｎ ＋１）（ ａｎ ＋１） ＝→　ａ^２ｎ^２＋２ａｎ＋１
　　　＝→　ｎ （ ａ^２ｎ ＋ ２ａ ）＋ １
　　　ｂ ＝ ａ^２ｎ ＋ ２ａ　と置くと、
　　　　　　ｍ^２ ＝ ｂｎ ＋ １
ｍ^３ ＝→ ｍ^２ × ｍ ＝→ （ ｂｎ ＋１）（ ａｎ ＋１）
　　　＝→　ａｂｎ^２＋（ａ＋ｂ）ｎ＋１
　　　＝→　ｎ｛ａｂｎ＋（ａ＋ｂ）｝＋１
　　　ｃ ＝ ａｂｎ＋（ａ＋ｂ） と置くと、
　　　　　　ｍ^３ ＝ ｃｎ ＋ １
ｍ^４ ＝→ ｍ^３ × ｍ ＝→ （ ｃｎ ＋１）（ ａｎ ＋１）
　　　＝→　ａｃｎ^２＋（ａ＋ｃ）ｎ＋１
　　　＝→　ｎ｛ａｃｎ＋（ａ＋ｃ）｝＋１
　　　ｄ ＝ ａｃｎ＋（ａ＋ｃ） と置くと、
　　　　　　ｍ^４ ＝ ｄｎ ＋ １
以上のように、どこまで行っても ｎ で割ると１余る数になるから、 ｍ^ｋ を ｎ で割ると１余ることが分かる。

【 別 解 】

２項定理より、
　　　
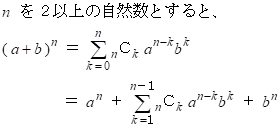
b ＝ 1 とすると、
　　　

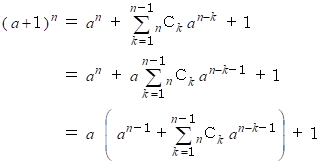
　（　）の中は自然数なので、( a+1 ) ⁿ は a で割ると１余る数である。
　 a を ｎ で割り切れる数とすると、
　a+1 は ｎ で割ると１余る数になる。
　また、 ( a+1 ) ⁿ は、 ｎ で割ると１余る数になる。
　したがって、ｎ で割ると１余る数を ｎ 乗したら、 ｎ で割ると１余る数になる

【 問 題 ２ 】

全体集合を 自然数 とする。
ｍ を ｎ で割ると１余り、 かつ、 ｈ を ｎ で割ると ｗ 余るとき、 ｍｈ を ｎ で割ると ｗ 余ることを証明せよ。

　【 解 答 】

次のように置く。
　　　ｍ　＝　ａｎ ＋ １　　　　ｈ　＝　ｂｎ ＋ ｗ
ｍｈ ＝ （ ａｎ ＋１）（ ｂｎ ＋ ｗ ） ＝→　ａｂｎ^２＋（ａｗ＋ｂ）ｎ＋ｗ
　　　＝→　ｎ｛ａｂｎ ＋ (ａｗ＋ｂ）｝＋ ｗ
ｃ ＝ ａｂｎ ＋ (ａｗ＋ｂ） と置くと、
　　　ｍｈ ＝ ｃｎ＋ｗ
したがって、 ｍｈ は ｎ で割ると ｗ 余る。

【 問 題 ３ 】

２²¹ を ５ で割るといくら余るか？

　【 解 答 】

　　　２^０ ＝ １　　２^１ ＝ ２　　２^２ ＝ ４　　２^３ ＝ ８　　２^４ ＝ 16
　２^４は５で割ると１余る数である。 よって、【 問 題１ 】より、（ ２^４ ）^５ は５で割ると１余る数である。 よって、 【 問 題 ２ 】より、（ ２^４ ）^５ × ２ は５で割ると２余る数である。
２²¹ ＝（ ２^４ ）^５ × ２　だから、２²¹ は５で割ると２余る数である。
したがって、 答えは ２ である。

　【 別 解 】

　２²¹　＝→　２ × ４¹⁰　＝→　２ ×（５−１）¹⁰
　　　　＝→　２ ×｛ ₁₀Ｃ_０ × ５¹⁰ ×（ −１ ）^０ ＋ ₁₀Ｃ_１ × ５^９ ×（ −１ ）^１
　　　　　　　　＋ ₁₀Ｃ_２ × ５^８ ×（ −１ ）^２ ＋ ・ ・ ・ ＋ ₁₀Ｃ₁₀ × ５^０ × （ −１ ）¹⁰ ｝
　　　　＝→　５ × ２ ×｛ ₁₀Ｃ_０ × ５^９ × （ −１ ）^０ ＋ ₁₀Ｃ_１ × ５^８ × （ −１ ）^１
　　　　　　　　＋ ₁₀Ｃ_２ × ５^７ ×（ −１ ）^２ ＋ ・ ・ ・ ＋ ₁₀Ｃ_９ × ５^０ × （ −１ ）^９ ｝
　　　　　　　　＋ 　２ × ₁₀Ｃ₁₀ × ５^０ × （ −１ ）¹⁰
したがって、 ２²¹ は５で割ると ２ × ₁₀Ｃ₁₀ × ５^０ ×（ −１ ）¹⁰ 余る数である。
２ × ₁₀Ｃ₁₀ × ５^０ ×（ −１ ）¹⁰　＝→　２　だから、 ２²¹ は５で割ると２余る数である。
したがって、 答えは ２ である。