(1) べき級数とは、無限母関数とは
-
べき級数とは、第 n 項が 係数 × x n−1 の形になっている数列の総和のことです。べき級数は、x を入力したときに、収束する場合は、収束値を出力する関数にもなります。
母関数 ( 生成関数 ) とは、x を入力したときに、とある数列の第 n 項に x n−1 をかけ、その総和をとったものを出力する関数です。要するに、係数は数列であるとの見解に立つ べき級数 のことであり、収束値を出力するものです。
-
無限数列: { 1 1 1 1 1 ・・・・ } の母関数は次のように表されます。
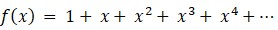
x = 0.8 のとき、この母関数の収束値を求めてみましょう。
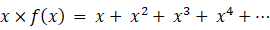

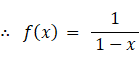
したがって、 f (0.8) = 5
-
x = 0.8 のとき、次の母関数の収束値を求めてみましょう。
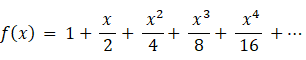
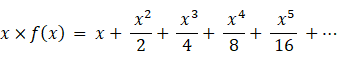
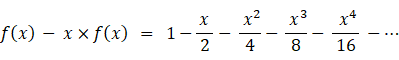
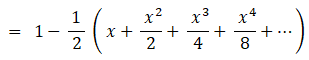
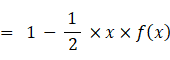
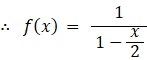
したがって、 f (0.8) = 1.6666…
一般的に、
-
a < 1 かつ x < 1 として、次の母関数の収束値を求めてみましょう。
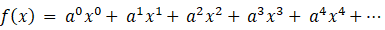
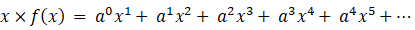
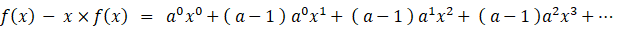
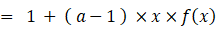
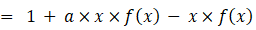
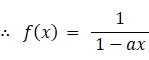
※ 参照: 数理論 > 等差数列 ・ 等比数列 の和
-
無限数列: { 1 1 1 1 1 ・・・・ } の母関数は次のように表されます。
f (x) = 1 + x + x2 + x3 + x4 + x5 + x6 + ・・・・
これから、次の式が成り立っていることを示します。

{ f (x) } 2 = 1 + 2x + 3x2 + 4x3 + 5x4 + 6x5 + ・・・・
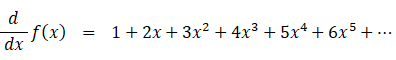
したがって、

ここで、(2)を思い出してください。すると、次の式が成り立っていることが分かります。

このことを利用して、次の無限数列の総和を求めてみましょう。
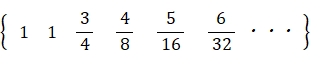
この数列を書き直すと、次のようになります。
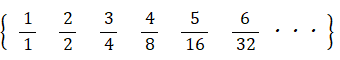
これは、無限数列: { 1 1 1 1 1 ・・・・ } の母関数の微分、つまり、次に式
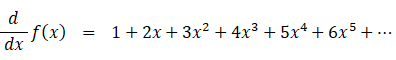
において、 x = 0.5 のときを表しています。したがって、この無限数列の総和は、次のようにして求めることができます。
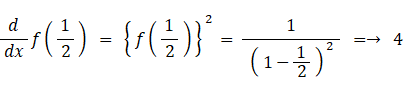
 数理論 へ戻る
数理論 へ戻る