正方形の畑の４か所にアリの巣があります。 （ Ａ 〜 Ｄ ）
　　　
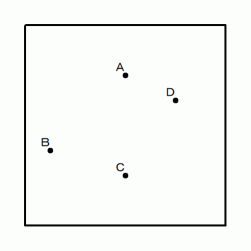
アリの移動の速さはすべて同じであるとします。 それぞれの巣から出発する時に他の巣のアリよりも早く辿り着ける場所を自分達の縄張りとします。 すると、 縄張りは次の図のように区分されます。
　　　
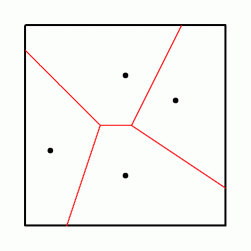
どうのようにして縄張り区分図は作成されたのでしょう？
まず、 最も離れている巣のペアを見つけます。 それは、 Ｂ と Ｄ です。
次に、 ３つの巣を頂点とする三角形を見つけますが、 そのときの条件として、 Ｂ と Ｄ が２つとも頂点となっている三角形は除きます。 すると、 △ＡＢＣ と △ＡＣＤ になります。
その次に、 ２つの三角形のすべての辺の垂直二等分線を描きます。 三角形の３つの辺の垂直二等分線は １ 点で交わります。 その交点は三角形の外接円の中心になっています。
　　　
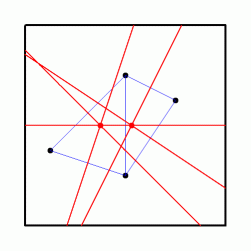
最後に、 それぞれの垂直二等分線から、 ３つの垂直二等分線の交点から辺に垂直に交わる線分のみを残して、 それ以外は消去します。