【 問 題 】
-
中心が原点にある半径が 25 の円の円周上に次の4点をとり、 直線で結んで四角形を作った。
A( −7, 24 ) B( −15,−20) C( 15,−20 ) D( 15, 20 )
この円に内接する四角形の面積はいくらか?
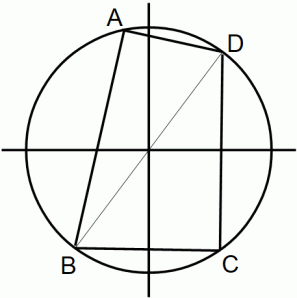
辺ABの長さ =
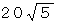
辺BCの長さ = 30
辺CDの長さ = 40
辺ADの長さ =
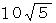
対角線BDはこの円の直径になっている。 したがって、 円周角の定理 より、 ∠BCD と ∠DAB は直角である。
したがって、 この四角形の面積 = △BCDの面積 + △DABの面積 より、
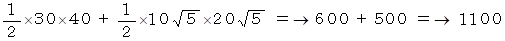
-
ブラフマグプタの公式 より、
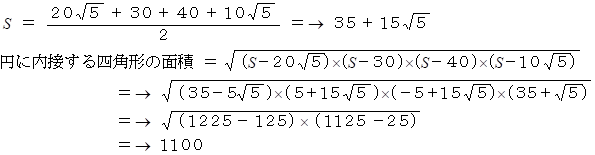
 幾何学 へ戻る
幾何学 へ戻る