（２） シンプソンの公式

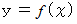　 の直交２次元座標上に曲線 があります。 その曲線の軸に対する正射影を考えると、 その陰になる部分の の区間 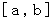においての面積が 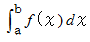になります。
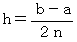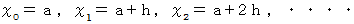　 小区間を とし、 とします。

　 プログラムで、 限られた区分数で少しでも誤差の少ない値を弾き出そうとするのならば、 小区間に対応する曲線を元の曲線に近い放物線に置き換えてから計算するという方法があります。
　 ３点 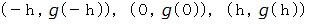を通る放物線を次のように置きます。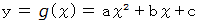
　　　　　
すると、
　　　　　
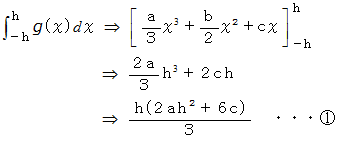
さて、 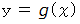が３点を通ることから、 次の３つの式が成り立ちます。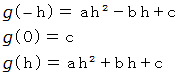
　　　　　
　　　　　
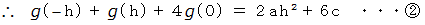
を に代入すると、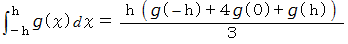
　　　　　

　 ３点 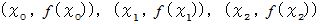を通る放物線を 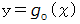とすると、 次のように近似することができます。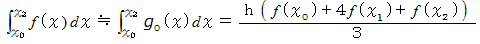
　　　　　
　 ３点 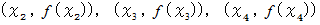を通る放物線を 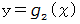とすると、 次のように近似することができます。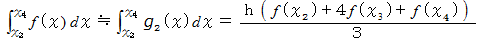
　　　　　
　このようにして、 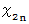まで全てを加え、 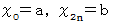とすると、 の区間 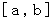の積分の近似値を求めることができます。 それは次のようになります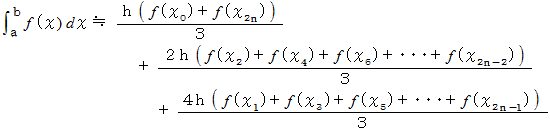
　　　　　
この近似式を、 シンプソンの公式と言います。

では、 どれくらいの誤差が少なくなっているのか、 プログラムを作って確かめてみましょう。