【 問 題 】

次の漸化式で与えられる数列の第 n 項の値（ a _n ）を n を用いて表せ。
　　　 a ₁　＝ 2
　　　

【 解 答 】

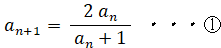
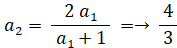
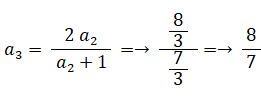
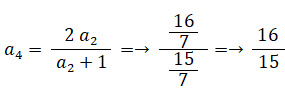
以上より、次の式が成り立つと予想される。
　　
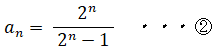
n ＝ 1　のとき、 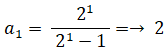となり、�Aは成り立つ。
n ＝ k　のとき�Aが成り立つと仮定する。つまり、次の式が成り立つと仮定する。
　　
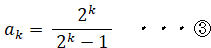
n ＝ k のとき、�@より次の式が成り立つ。
　　
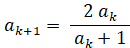
この式に�Bを代入して、
　　
　　　　　　
　　　　　　
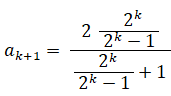
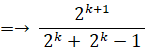
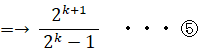
以上より、�Bが成り立つならば�Dが成り立つことがわかった。

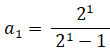　 が成り立つから、 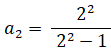が成り立つ。
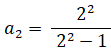　 が成り立つから、 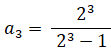が成り立つ。
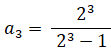　 が成り立つから、・・・・ というふうにして、
すべての自然数 n ついて�Aの式が成り立つことが分かる。

したがって、答えは �Aの式である。