長方形ＡＢＣＤの中に無作為に点Ｐを取り各頂点と直線で結ぶ。
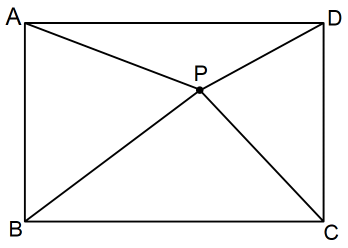
このとき、△ＡＰＤの面積 と △ＢＰＣの面積 の合計は □ＡＢＣＤの面積 の半分になっていることを示そう。

　　
　　　　　　　　　　　　　ＡＤに平行にＥＦを引く
　　
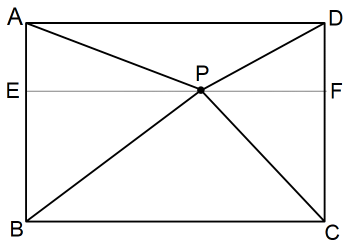
　　　　　　　　　　　　　点ＰをＦまで移動する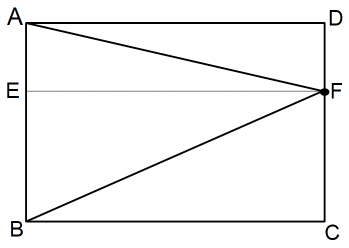
　　

　　△ＡＰＤ ＝ △ＡＦＤ ＝ △ＦＡＥ
　　△ＢＰＣ ＝ △ＢＦＣ ＝ △ＦＢＥ
　　（ △ＡＰＤ ＋ △ＢＰＣ ）× ２　＝　△ＡＰＤ ＋ △ＡＰＤ ＋ △ＢＰＣ ＋ △ＢＰＣ
　　　　　　　　　　　　　　　　　＝　△ＡＦＤ ＋ △ＦＡＥ ＋ △ＢＦＣ ＋ △ＦＢＥ
　　　　　　　　　　　　　　　　　＝　□ＡＢＣＤ

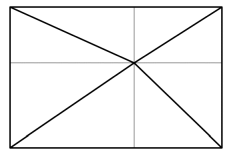
（ 別 解 ）
　　　　補助線を２つ引けば一目瞭然かも。