(1)
-
3 7 19 55 ・ ・ ・ ・
上記の数列は次の漸化式で与えられます。
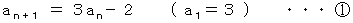
第 n 項は次の式で与えられます。
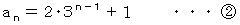
 から
から  を導いてみましょう。
を導いてみましょう。まず、
 より、 次のような形にならないか考えてみることにします。
より、 次のような形にならないか考えてみることにします。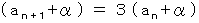
変形すると、
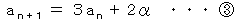
 と
と  を比べて、
を比べて、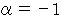
したがって、
 の式は、 次のように変形できることが解りました。
の式は、 次のように変形できることが解りました。
ここで、
 と置くと、
と置くと、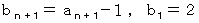 なので、
なので、  は次のように変形できます。
は次のように変形できます。
これは、 初項 2 、 公比 3 の等比数列の漸化式なので、
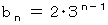
したがって、
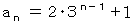
( 問 題 )
-
1 9 61 369 2101 ・ ・ ・ ・
上記の数列は次の漸化式で与えられます。

第 n 項はどんな式で与えられますか?
 を変形すると、 次のようになります。
を変形すると、 次のようになります。
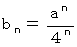 と置くと、
と置くと、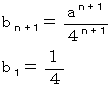
したがって、
 は、
は、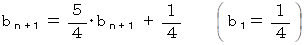
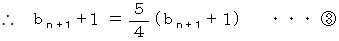
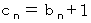 と置くと、
と置くと、
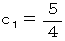
したがって、
 は、
は、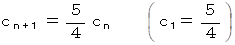
上記の式は、 初項
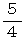 、 公比
、 公比 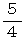 の等比数列の漸化式だから、
の等比数列の漸化式だから、
したがって、
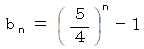
したがって、
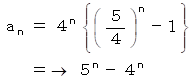
( 問 題 )
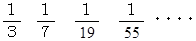
上記の数列は次の漸化式で与えられます。
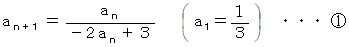
第 n 項はどんな式で与えられますか?
-
an や an + 1 は 0 ではないので、
 を変形すると、 次のようになります。
を変形すると、 次のようになります。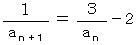
 と置くと、
と置くと、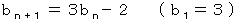
(1)より、
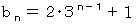
したがって、

【 問 題 】
-
4 10 20 42 100 ・ ・ ・ ・
上記の数列は次の漸化式で与えられます。
an+1 = 3an − 8n + 6 ( a1 = 4 )
第 n 項はどんな式で与えられますか?
-
an+1 = 3an − 8n + 6 は次のように変形することができる。
an+1 − 4( n + 1 )+ 1 = 3( an − 4n + 1 )
bn = an − 4n + 1 と置くと、 上式は次のようになる。
bn+1 = 3bn
また、 b1 = a1 − 4 + 1 =→ 1
したがって、 bn = 3 n−1
よって、 an − 4n + 1 = 3 n−1
よって、 an = 3 n−1 + 4n − 1
 数理論 へ戻る
数理論 へ戻る