( 問 題 )
-
1 〜 n までの自然数があり、 無作為に1個ずつ自然数を抽出していく。 毎回 1 が選ばれる確率は n 分 の 1 である。 すべての数が揃うまでに平均何個の数を集めなければならないか? すべての数が揃うまでに抽出する数( すう )の数 ( かず ) の期待値を求めなさい。
( 一万回試行 のシミュレーション )
( 解 答 )
-
1 〜 n までの自然数、 1回あたりゲットできる確率は、 すべて 1 / n である。 x 種類の数を取得しているときに、 すべての数が揃うまで新たに抽出する数の数の期待値を
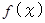 とする。 次のトライアルで新しい数を手に入れる確率は
とする。 次のトライアルで新しい数を手に入れる確率は 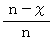 なので、
なので、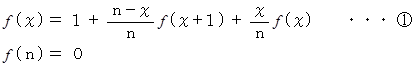
※
 の右辺は、1回トライアルした後の期待値を表している。第2項目は、次のトライアルで新たな数をゲットした場合に、すべての数が揃うまで新たに抽出する数の数の期待値 に 次のトライアルで新たな数をゲットする確率をかけたもので、第3項目は、次のトライアルで新たな数をゲットできなかった場合に、すべての数が揃うまで新たに抽出する数の数の期待値 に 次のトライアルで新たな数をゲットできない確率をかけたものである。
の右辺は、1回トライアルした後の期待値を表している。第2項目は、次のトライアルで新たな数をゲットした場合に、すべての数が揃うまで新たに抽出する数の数の期待値 に 次のトライアルで新たな数をゲットする確率をかけたもので、第3項目は、次のトライアルで新たな数をゲットできなかった場合に、すべての数が揃うまで新たに抽出する数の数の期待値 に 次のトライアルで新たな数をゲットできない確率をかけたものである。 より、
より、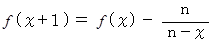
したがって、
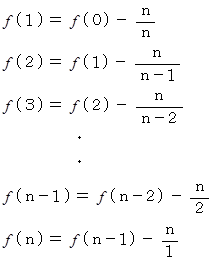
上記の式たちを辺々加えると、
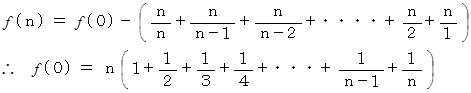
上記の式が答えである。
-
n 種類のうち既に m 種類が出ているとき、 1回試行当たりに新しい種類を獲得できる確率を P( m ) とすると、
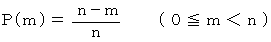

n 種類のうち既に m 種類が出ているとき、 さらに新たな種類を獲得するための試行回数の期待値 E( m ) は、 次の式になる。
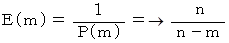
したがって、 n 種類すべてを獲得するための試行回数の期待値は、 次の式で表される。
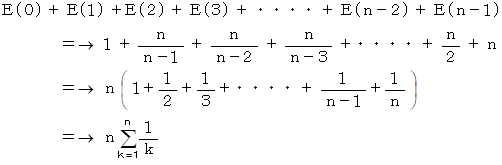
 確率 へ戻る
確率 へ戻る