単振動を説明するとき、「 平面上で原点を中心とする半径１の円周上を反時計回りに等速円運動をしている質点の位置の縦軸成分のみを取り出して、動きを見ていく。」といった方法をとりますが、それを、複素平面で反対方向に等速回転しているベクトルの合成として見る方法を紹介します。

　複素ベクトル（ e ^iθ ）の実数成分（ cos θ ）は、次のように表されます。
　　　
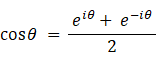
この式は、次のようにして導かれます。

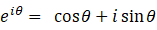
θ を −θ で置き換えると、
　　
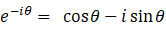
辺々を加えて、
　　
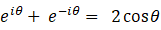
よって、
　　

　θ を横軸に、cosθ を縦軸とって、θ を一定の速さで大きくしていくと、cosθ は振幅２の単振動をしてサインカーブのグラフを描きます。また、複素平面上で θ を一定の速さで大きくしていくと、原点を中心に、複素ベクトル e ^iθ は反時計回りに等速円運動をし、複素ベクトル e^−iθ は時計回りに等速円運動をします。そして、この２つの複素ベクトルを合成すると、合成ベクトルの終点は実数軸上を振幅４で単振動します。

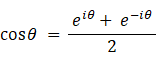
　単振動の振動数を ω / 2π ( ω は角速度の大きさ ) で表し、時間を t で表わすと、e ^iθ ＝ e ^iωt　になります。 e ^iωt を時間で微分すると iω e ^iωt になります。これは、複素ベクトルの時刻 t における速度を表します。これは、角速度の大きさ ω で反時計回りに等速回転している複素ベクトル e ^iωt の時刻 t における速度は、向きが複素ベクトルを時計回りに90度回転させた向きで、大きさが ω になっていることを示しています。このことをイメージすると、大きさ１の複素ベクトル e ^iωt が反時計回りに角速度の大きさ ω で等速回転しているアニメが浮かんできます。