【 問 題 】

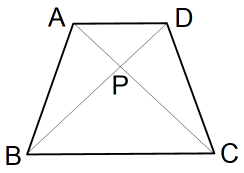
台形ＡＢＣＤがある。２つの対角線の交点をＰとする。

　　（１） △ＡＰＤ と △ＢＰＣ が相似であることを示せ。

　　（２） △ＡＰＢ と △ＤＰＣ の面積が等しいことを示せ。

　　　　　　　　　

【 解 答 】

（１）
　　　∠ＡＰＤ ＝ ∠ＣＰＢ
　　　∠ＰＡＤ ＝ ∠ ＰＣＢ
　　　∠ＰＤＡ ＝ ∠ ＰＢＣ
　　　よって、△ＡＰＤ と △ＢＰＣ は相似である。


（２）
　　　△ＡＢＣ と △ＤＢＣ の面積は等しい。
　　　なぜなら、底辺の長さも高さも等しいから。
　　　△ＡＰＢ と △ＤＰＣ はこれら２つの三角形から
　　共通部分の△ＰＢＣを除外した部分である。
　　　よって、△ＡＰＢ と △ＤＰＣ の面積は等しい。