【 問 題 】

台形ＡＢＣＤがある。対角線の交点をＰとする。
　　　
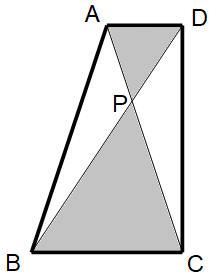
　　　∠ＢＣＤ ＝ 90°　　　∠ＡＤＣ ＝ 90°
　　　ＡＤ ＝ 4 cm　　　ＢＣ ＝ 8 cm　　　ＣＤ ＝ 12 cm

灰色の部分の面積を求めよ。

【 解 答 】

台形ＡＢＣＤの面積は、 ( 4＋8 ) × 12 ÷ 2 ＝→ 72 cm²
△ＰＤＡ ＝ x cm² とする。
△ＰＤＡ と △ＰＢＣ は相対する３つの角が等しいので相似であり、その比は １：２ である。
よって、
　　　ＰＢ ＝ ２×ＰＤ　　　ＰＣ ＝ ２×ＰＡ
　　　△ＰＢＣ ＝ ４×△ＰＤＡ ＝→ 4 x cm²
△ＡＰＤ と △ＡＰＢ は高さが等しい三角形なので、 △ＡＰＢ ＝ 2 × △ＡＰＤ ＝→ 2 x cm²
△ＤＰＡ と △ＤＰＣ は高さが等しい三角形なので、 △ＤＰＣ ＝ 2 × △ＤＰＡ ＝→ 2 x cm²

したがって、
　　　x cm² ＋ 4 x cm² ＋ 2 x cm² ＋ 2 x cm² ＝ 72 cm²
　　　よって、 9 x cm² ＝ 72 cm²
よって、 x ＝ 8
したがって答えは、
　　　x cm² ＋ 4 x cm²　＝→　5 x cm²　＝→　40 cm²