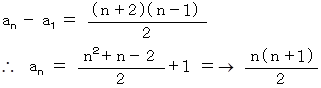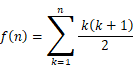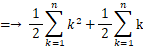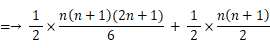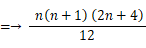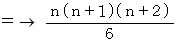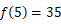団子ピラミッド （ 四面体数 ） 数理論 へ戻る
大学生のための数学 へ戻る

2020.01.28_____

---

【 問 題 】

規格が同じ団子が沢山あります。 15 個 の団子を上から見て下図のように並べました。
　　　
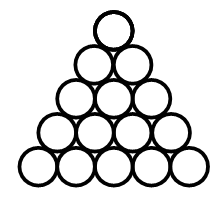
　 この上に隙間無く団子を積み上げていき 「 団子ピラミッド （ 正四面体 ）」 を作ったとき、
使用している団子の数はいくつでしょうか？

【 解 答 】

上から n 段目　　　１　　２　　３　　４　　５
n 段目の団子数 　　１　　３　　６　　10　　15
　　　　　　　　したがって、 答えは　35 個　です。

もっとスマートな解法は、 次のようになります。
上からｎ段目の団子の数を ａ_ｎ とすると、
　　　ａ_ｎ − ａ_ｎ−１ ＝ ｎ
　　　ａ_ｎ−１ − ａ_ｎ−２ ＝ ｎ−１
　　　ａ_ｎ−２ − ａ_ｎ−３ ＝ ｎ−２
　　　　　　・
　　　　　　・
　　　　　　・
　　　ａ_３ − ａ_２ ＝ ３
　　　ａ_２ − ａ_１ ＝ ２
辺々加えて、
　　　

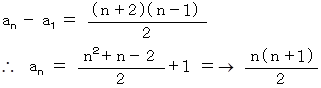
上から n 段目までの団子の総数を f (n) とします。
　　　
　　　　　
　　　　　
　　　　　
　　　　　
　　　
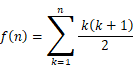
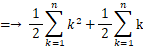
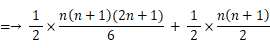
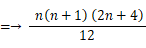
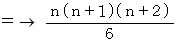
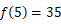
したがって、 答えは　35 個　です。