基礎物理学 へ戻る（１） 音のドップラー効果
-
音源 と 風 と 観察者 があります。
音源の観察者に対する方向をプラスとします。
観察者は静止しています。
風は、 音源の観察者に対する方向に、 観察者に対して速さ
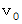で吹き続けています。音源は、 音源の観察者に対する方向に、 観察者に対して速さ
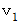で遠ざかっています。空気中の音の速さを
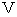とします。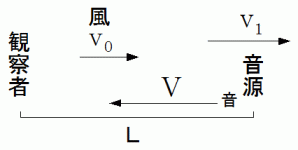
音源は、 １ 秒毎に、 一瞬だけ振動数
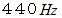の音を発します。 このとき、 観察者が聞く音の間隔は、 １ 秒ではないことを今から示します。 最初の音を音源が発した時刻を０秒とし、 そのときの音源と観察者の間隔を 
とします。この音を観察者が聞く時刻 ：
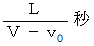
２回目の音を観察者が聞く時刻 ：
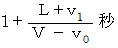
３回目の音を観察者が聞く時刻 ：
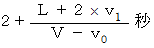
回目の音を観察者が聞く時刻 ：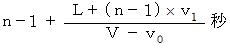
観察者が
回目の音を聞いてから次に 
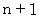回目の音を聞く時間を求めます。
今は、 観察者が静止しているとしましたが、 今度は、 風がなくて、 観察者が音源の観察者に対する方向に地面に対して速さ
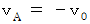で移動していて、 音源が音源の観察者に対する方向に地面に対して速さ 
で移動しているものとしましょう。一般的な図 ：
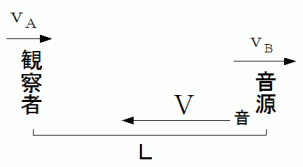
今回のケースの図 ：
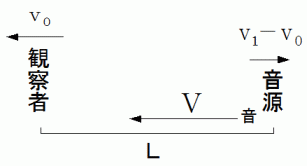
このとき、 観察者からすると、 風は、 音源の観察者に対する方向に、 観察者に対して速さ
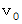で吹き続けていて、 音源は、 音源の観察者に対する方向に、 観察者に対して速さ 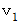で移動し、 観察者から遠ざかっています。 ということは、 最初の設定と全く同じということです。 したがって、 このとき観察者が聞く音の間隔は、 さきほどの式に代入して、 次のようになります。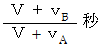
さて、 今度は、 今の設定を次のように変えてやります。 他は同じです。
「 音源は、ずっと
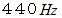の音を発し続けます。」すると、 このとき観察者が聞く音の振動数は
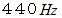ではなく、 次のようになります。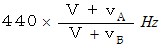
※ Ｖ は音速 ｖA は観察者の速さ ｖB は音源の速さ
※ 観察者も音源も音の伝わる方向に対して反対方向に移動している場合__
※ 無風という条件下 もし、速さ ｖ0 の追い風がある場合は Ｖ に ｖ0 を足す必要あり。
これが、 ドップラー効果の式です。 先ほどの式と分母分子が反対になっています。 速度の向きを、 観察者から音源へと向かう方向をプラスにした場合の式になっています。 無風の条件下の式になっています。
音のドップラー効果については、 音源と観察者との相対速度さえ解ればその程度が解るというものではありません。 その上に、 観察者 の 音の媒体としての空気 に対する速度のデーターが必要になってきます。 このことは、 「 無風の条件下で、 音源と観察者の距離が変化しているときに、 音源が移動しているのか観察者が移動しているのかを区別をして考える。」 ということで一般化されています。
十進BASIC で、 ドップラー効果でどれくらい音程が変化するのかを体験するプログラムを作ってみました。