光源 と 観察者 があります。
光源の観察者に対する方向をプラスとします。
観察者は静止しています。
光源は、 光源の観察者に対する方向に、 観察者に対して速さ
で遠ざかっています。光の速さを
とします。光源は、 １ 秒毎に、 一瞬だけ振動数
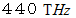の光を発します。このとき、 観察者が見る光の間隔は、 １ 秒ではないことを今から示します。
最初の光を光源が発した時刻を０秒とし、 そのときの光源と観察者の間隔を
とします。この光を観察者が見る時刻 ：
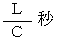
２回目の光を観察者が見る時刻 ：
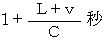
観察者が
回目の光を見てから次に 
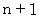回目の光を見る時間を求めます。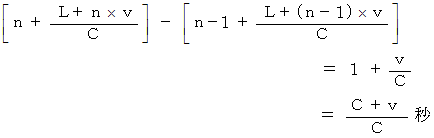
さて、 今度は、 今の設定を次のように変えてやります。 他は同じです。
「 光源は、 ずっと
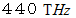の光を発し続けます。」すると、 このとき観察者が見る光の振動数は
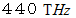ではなく、 次のようになります。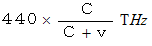
これが光のドップラー効果の式です、 と言いたいところですが、 残念ながらこの式は間違っています。 相対性理論によりますと、 光はドップラー効果以外に、 観察のされ方によって振動数が変わることがあるのです。 それは光源の 「 時の経過スピード 」 と 観察者の 「 時の経過スピード 」 が異なるために起こってきます。 観察者にとって速さ
で移動している光源の 「 時の経過スピード 」 は、 観察者の 「 時の経過スピード 」 に比べて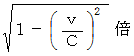 
と小さくなっています。 ということは、 移動している光源で発生する光はゆっくりと振動するということなので、 振動数も 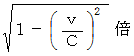に小さくなっているということです。 したがって、 光のドップラー効果の式は次のようになります。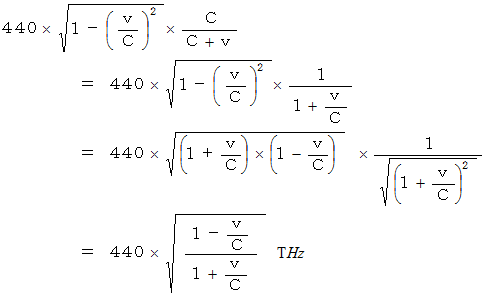
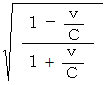は、 が正の数のときは １ より小さく、 また、 が負の数の時は １ より大きくなりますので、 観察者と光源が遠ざかっているときは、 観察者が見る光の振動数は 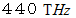よりも小さく、 観察者と光源が近づいているときは、 観察者が見る光の振動数は 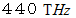よりも大きくなることが解ります。 振動数が大きい光ほど、 波長が短くて紫外線の波長に近づきます。
この論文のトップへ戻る