【 問 題 】

　 正方形に内接する四角形の２つの対角線が直交するとき、 ２つの対角線の長さが等しいことを証明せよ。

　　　　

　【 解 答 】

　　　　


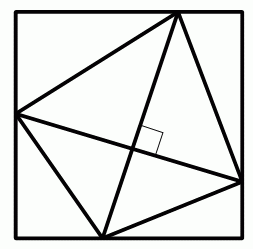
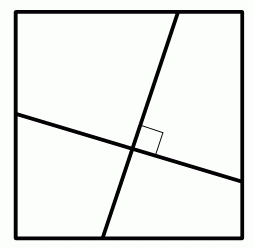
上図の２つの対角線を平行移動して、 下図のようにし、 記号を付ける。

　　　　

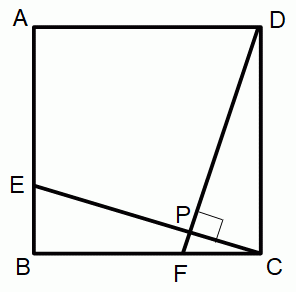
ＥＣ ＝ ＤＦ であることを証明するためには、 △ＣＥＢ と △ＤＦＣ が合同であることを示せばいい。
四角形ＡＥＰＤ の内角の和は 360 度 なので ∠ＡＥＰ と ∠ＡＤＰ の和は 180 度 である。
よって、 ∠ＣＥＢ ＝ ∠ＡＤＰ
∠ＤＦＣ ＝ ∠ＡＤＰ
よって、 ∠ＣＥＢ ＝ ∠ＤＦＣ
よって、 ∠ＢＣＥ ＝ ∠ＣＤＦ
ＢＣ ＝ ＣＤ
以上より、 △ＣＥＢ と △ＤＦＣ は合同であることが分かる。
よって、 ＥＣ ＝ ＤＦ

　【 解 説 】

　「 正方形の対辺を結ぶ直交する２つの線分の長さは等しい。」という性質をつかえば、 「 与えられた４点がすべて辺上にあるように正方形を描け 」 という問題を解決することができます。