エジプト分数とは、単位分数の和のことです。

【 問 題 １ 】

x ≧ y ≧ z を満たす自然数のトリオ ( x , y , z ) のうち、次の式を満たすものを３組以上示せ。
　　　

　【 解 答 】

　　
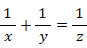
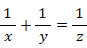
よって、
　　
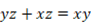
よって、
　　
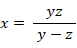
y ＝ n ＋ 1 ，　z ＝ n　と置くと、上式より　x ＝ n ( n ＋ 1 )　となるので、次の式が成り立つ。
　　

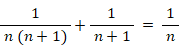
n ＝ 2，3，4 のときを例として３組記述すると、
　　( x , y , z ) ＝ ( 6, 3, 2 )，( 12, 4, 3 )，( 20, 5, 4 )

それ以外の例としては、次の組など無数に存在します。
　　( x , y , z ) ＝ ( 2, 2, 1 )，( 4, 4, 2 )，( 6, 6, 3 )，( 12, 12, 6 )

【 問 題 ２ 】

x ≦ y ≦ z を満たす自然数のトリオ ( x , y , z ) のうち、次の式を満たすものを３組示せ。
　　　

　【 解 答 】

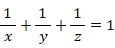
　x ≧ 4　のとき、
　　　
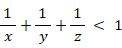
　　　したがって、問題の式を満たす x は存在しない。
　x ＝ 1　のとき、
　　　
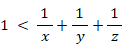
　　　したがって、問題の式を満たす x は存在しない。
　x ＝ 3　のとき、
　　　( x , y , z ) ＝ ( 3, 3, 3 )
　x ＝ 2　のとき、
　　　次の式を満たす y と z のペアを探す。
　　　　　
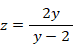
　　　すると、次の２組が見つかる。
　　　　　( x , y , z ) ＝ ( 2, 3, 6 )，( 2, 4, 4 )

　というわけで、答えは、
　　　( x , y , z ) ＝ ( 2, 3, 6 )，( 2, 4, 4 )，( 3, 3, 3 )