【 問 題 】

　円の円周上に点を７個とって、全ての点どうしを結んで直線分（弦）を引きます。
そのときに、１点で３つ以上の直線分が交わることが無いようにします。

　　（１） 弦は全部で何個あるでしょうか？

　　（２） 弦が交わる交点は全部で何個あるでしょうか？

　　（３） 円はいくつの領域に分割されるでしょうか？

【 解 答 】

（１）
　　　₇Ｃ₂　＝→　21 (個)


（２）
　　　４個の点を選ぶと１点でクロスする２つの線分の組がチョイスできます。
　　　ということは、交点の数は、７個の点から４個の点を選ぶすべての組み合わせの数に等しいです。
　　　よって答えは、 ₇Ｃ₄　＝→　( 7×6×5×4 ) ÷ ( 4×3×2 )　＝→　35 (個)


（３）
　円の円周上に n 個の点を取り、それらを直線分で結びます。必ずしも全ての点どうしを結ぶ必要はありません。直線の交点も含めて、点から複数の直線や曲線が出ているところを頂点ということにし、頂点と隣の頂点とを結ぶ線を辺ということにし、辺で全周を囲まれる領域を面ということにします。
　そして、頂点の数を v 個，辺の数を e 個，面の数を f 個 とすると、 f ＝ 1 ＋ e − v　という式が成り立ちます。

　　　　　　

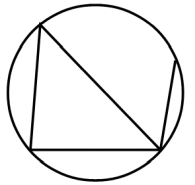
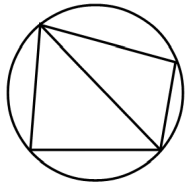
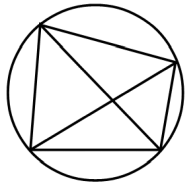
　円の円周上に n 個の点を取り全ての点どうしを結んで直線分を描きます。そのときに、１点で３つ以上の直線分が交わることが無いようにします。
すると、弧が n 個できます。
そのとき、弦は _nＣ₂ 個あります。
また、弦の交点は _nＣ₄ 個あります。
直線分で構成される辺は何個になるでしょう？
弦の端点から出発して弦の上を移動していくと、交点を通過するたびに辺の数が１個ずつ増えていきます。1 本の弦に交点が k 個あるとすると、出発時点に 1 個だった辺が最終的には k＋1 個になります。
1 個の交点が 2 本の弦にあるので、直線分で構成される辺は全部で _nＣ₂ ＋ 2 _nＣ₄ 個あることになります。

v ＝ n ＋ _nＣ₄
e ＝ n ＋ _nＣ₂ ＋ 2 _nＣ₄
したがって、
　　　f ＝ 1 ＋ _nＣ₂ ＋ _nＣ₄
この式に n＝7 を代入して、答えは 57 の領域になります。

ちなみに、 n＝4 を代入すると、 f＝8 になります。