【 問 題 １ 】

　 半径の大きさの比が １ ： ２ の２つの円があります。 小さい方の円を大きい方の円の中から内接させます。 大きい方の円に直径となる線分を １ 本引きます。 それを下の図とします。 Ｏ_１ は大きい方の円の中心で、 Ｏ_２ は小さい方の円の中心です。
　　　　　　図−１
　　　　　　　

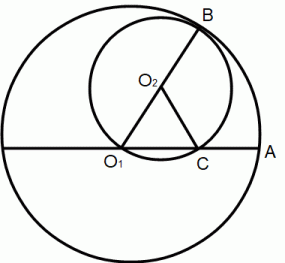
（１）
　弧ＡＢの長さと弧ＣＢの長さが等しいときに、 ∠ＢＯ_２Ｃ は ∠ＢＯ_１Ａ の２倍であることを証明しなさい。


（２）
　タレスの定理を用いずに、 ∠ＢＣＯ_１ は直角であることを示しなさい。

【 解 答 】

（１）
　∠ＢＯ_１Ａ を θ_１ と、 ∠ＢＯ_２Ｃ を θ_２ とする。 小さい方の円の半径の大きさを ｒ とする。
　 　すると、 題意より次の式が成り立つ。
　　　　　　　２ｒθ_１　＝　ｒθ_２
　 　よって、　２θ_１　＝　θ_２


（２）
　∠ＢＣＯ_１　＝　∠ＢＣＯ_２　＋　∠Ｏ_１ＣＯ_２
　 　よって、　∠ＢＣＯ_１　＝　 ｛ （ 180°− ２θ ） ÷ ２ ｝ ＋ θ　＝→　90°


　 図−１ において、 小さい方の円を大きな円との内接を保ったまま、 反時計方向に滑らせることなく転がしていくと、 小さい方の円の点Ｂにおける接触点は大きい方の円の点Ｂを通る直径上を移動することを理解してください。