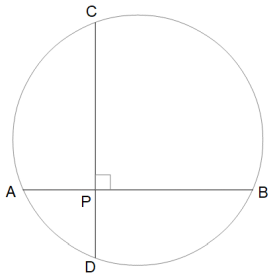
円の半径 ＝ r　　PA = a　　PB = b　　PC = c　　PD = d　とすると、次の式が成り立ちます。
　　　　4r² ＝ a² + b² + c² + d²

（証明）

ABに平行な直径 と CDに平行な直径 を作図します。
　　　

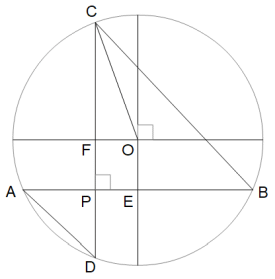
OC = r　　FO = PE　　∠CFO = ∠APD = 90°
PA+PB = 2×(PA+PE)　→　PE = (PB−PA)/2
PC+PD = 2×CF　→　CF = (PC+PD)/2
方べきの定理：
　　　円周角の定理より　∠DAB = ∠DCB　　∠ADC = ∠ABC
　　　よって、 △PAD と △PCB は相似。
　　　よって、 PA : PC = PD : PB　→　PA×PB = PC×PD
OC² ＝ CF² + OF² より、 r² ＝ (PC+PD)²/4 + (PB−PA)²/4
よって、 4 r² ＝ PC² + PD² + PB² + PA² + 2×(PC×PD−PA×PB)
よって、 4 r² ＝ PC² + PD² + PB² + PA²
よって、 4r² ＝ a² + b² + c² + d²