【 問 題 】

　　

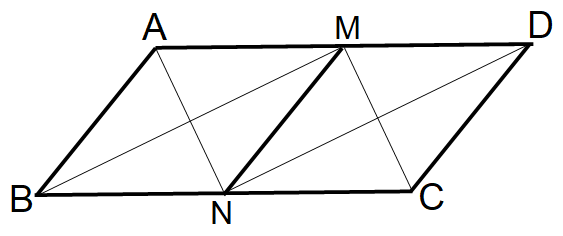
平行四辺形ABCDがあり、AD＝2ABである。ADの中点をM、BCの中点をNとする。
∠BMC＝90° を証明せよ。

【 解 答 】

AB と MN と DC は平行。 AD と BC は平行。
∠ABN ＝ ∠MNC　かつ　AB ＝ MN ＝ DC ＝ AM ＝ BN ＝ MD ＝ NC　だから、
　　□ABNM と □MNCD は合同な菱形である。
NB ＝ NM ＝ NC　だから、点B,M,C は　Nを中心とする同一円周上に存在する。
よって、円周角の定理より、∠BMC ＝90°

【 別解答 】

途中までは同じで、□ABNM と □MNCD は合同な菱形であること言う。
BM // ND ，AN // MC ，AN ⊥ BM ，MC ⊥ ND を示すことによって、
∠BMC＝90° を証明する。