【 問 題 】

　　　　１　　１　　２　　３　　５　　８　　13　　21　・ ・ ・ ・

フィボナッチ数列とは、 初項（ ａ_１ ）と 第２項（ ａ_２ ） が 1 で、 次の漸化式を満たす数列のことです。
　　　　
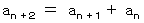
次の式が成り立ちことを証明なさい。
　　　　

【 解 答 】

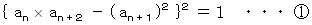
ｎ ＝ ｋ のとき、 式 が成り立つと仮定する。 つまり、 次の式が成り立つと仮定する。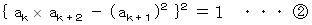
　　　　
さて、 このとき　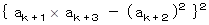　の値を求めることにする。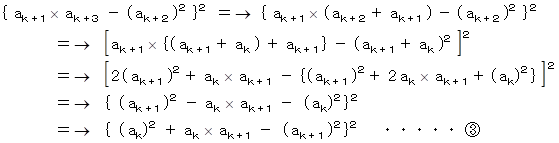
　　　　
ところで、 式 より、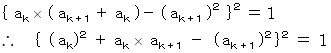
　　　　
したがって、 式 は次のようになる。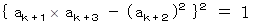
　　　　
　 以上より、 ｎ ＝ ｋ のときに 式 が成り立つと仮定すると、 ｎ ＝ ｋ＋１ のときも 式 が成り立つことが判った。
　 さて、 ｎ ＝ １ のとき、 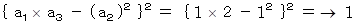となって、 式 が成り立つ。
　 ということは、 ｎ ＝ ２ のときも 式 が成り立つ。 ということは ｎ ＝ ３ のときも式 が成り立つ。 というふうに考えていくと、 式 はすべての自然数 ｎ について成り立っていることが判る。