1 1 2 3 5 8 13 21 ・ ・ ・ と続く数列は、 フィボナッチ数列と言われ、 次のような漸化式を持ちます。
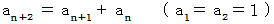
フィボナッチ数列の第
 項目の値は、 黄金比を
項目の値は、 黄金比を 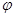 とすると、 次のように表されます。
とすると、 次のように表されます。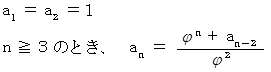
このことを証明してみましょう。
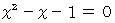 の正の解が黄金比ですから、 黄金比を
の正の解が黄金比ですから、 黄金比を 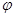 とすると、次の式が成り立ちます。
とすると、次の式が成り立ちます。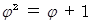
そこで、
 が 3 および 4 のときを 具体的に見てみましょう。
が 3 および 4 のときを 具体的に見てみましょう。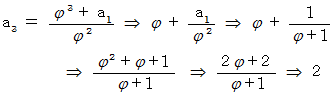
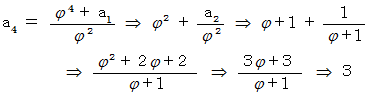
以上のようにきちんとフィボナッチ数列になっていることが解ります。 問題は
 が 5以上のときもすべてこの式が成り立っているかごどうかです。 そこで、 次のように置きます。
が 5以上のときもすべてこの式が成り立っているかごどうかです。 そこで、 次のように置きます。
すると、 次のようになります。
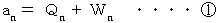
まず、
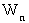 について考えます。
について考えます。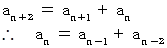
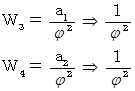

続いて、
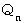 の部分について考えます。
の部分について考えます。したがって、 次の式が成り立ちます。
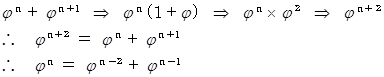
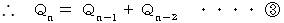

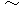
 より、
より、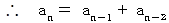
したがって、 この数列は次のような漸化式が成り立つことが解ります。
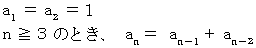
以上のような漸化式が成り立つ数列は、 フィボナッチ数列です。
フィボナッチ数列 と 黄金比 との出会いは、 これが初めてではありません。 私の別の論文 「 フィボナッチ数列 」 をご覧ください。 その中の
 の式を変形すると、 次のようになります。
の式を変形すると、 次のようになります。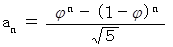
この式も、 フィボナッチ数列が黄金比を用いて表されています。
では、 逆に、 黄金比をフィボナッチ数列を用いて表すことはできないものでしょうか? できます。 私の別の論文 「 黄金比 」 を見ていただくとわかるのですが、 黄金比を連分数を使って表し、 それから黄金比の近似値を求める作業をしていきますと、 黄金比はフィボナッチ数列を用いて次のように表されることが解ります。
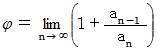
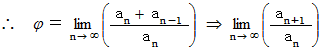

 数理論 へ戻る
数理論 へ戻る