1 1 2 3 5 8 13 21 ・ ・ ・ と続く数列は、 フィボナッチ数列と言われ、 次のような漸化式を持ちます。
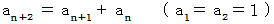
フィボナッチ数列の n項目の値 と n項目までの和 を求めてみましょう。
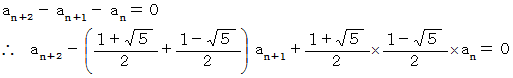
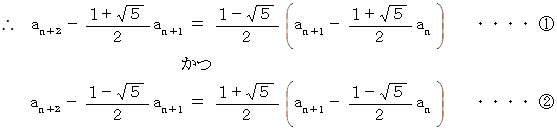
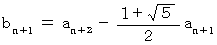 と置くと、
と置くと、 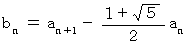 ですから、
ですから、  は次のようになります。
は次のようになります。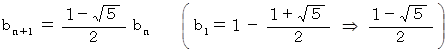
これは、 初項
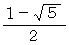 公比
公比 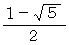 の等比数列です。 初項 d 公比 r の等比数列の場合、 n項目は
の等比数列です。 初項 d 公比 r の等比数列の場合、 n項目は 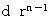 ですから、 この等比数列のn項目の値は次のようになります。
ですから、 この等比数列のn項目の値は次のようになります。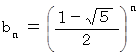
したがって、
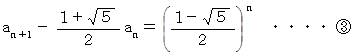
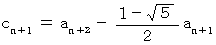 と置くと、
と置くと、 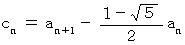 ですから、
ですから、  は次のようになります。
は次のようになります。
これは等比数列で、 n項目の値は次のようになります。
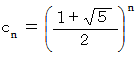
したがって、
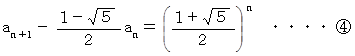
ちなみに、
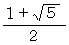 は 「 黄金比 」 です。
は 「 黄金比 」 です。さて、
 から
から  を辺々引くと、
を辺々引くと、
これで、 フィボナッチ数列の n項目の値 が解りました。
次は、 n項目までの和 を求めてみましょう。
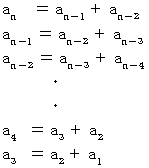
辺々加えると、
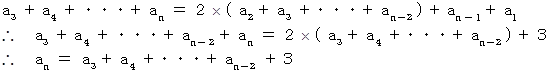
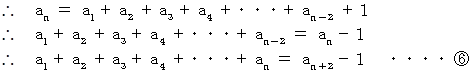
以上、
 と
と  が今回求めたかった式です。
が今回求めたかった式です。 数理論 へ戻る
数理論 へ戻る