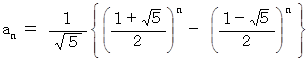
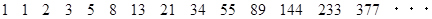
上記のフィボナッチ数列の隣り合う2つの数の2乗の和は、フィボナッチ数列を構成する数の1つになっています。例えば次のようにです。
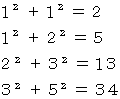
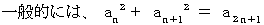
このことを証明してみましょう。
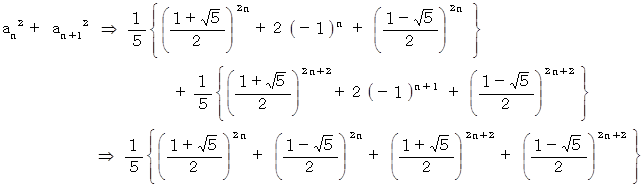
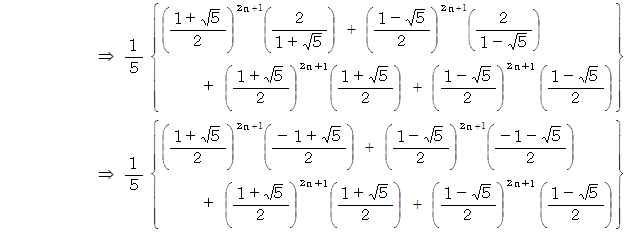
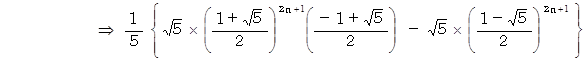
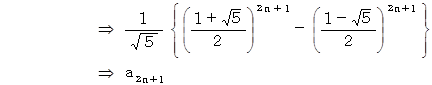
以上で証明を終わります。
さて、 10段の階段を2つ以上飛ばさずに上る場合の数を考えましょう。 数理論 > フィボナッチ数列の例 をご覧になればいいのですが、 答えは、 准フィボナッチ数列( 初項の1が抜け落ちたもの )の10項目の数で、89 です。
5段目を使用せずにゴールする場合 と 5段目を使用してゴールする場合 とに分けて考えます。 n 段の階段の上がり方の場合の数を
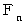 とすると、 次のように表されます。
とすると、 次のように表されます。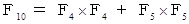
もし、 准フィボナッチ数列ではなくて、 フィボナッチ数列だったなら、 上式は次のようになります。
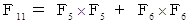
 数理論 へ戻る
数理論 へ戻る