1 から 5k までの 5k 個の自然数の要素で構成される集合があります。
この集合の部分集合( 空集合や全体集合を含める )が何個あるかというと、25k 個 です。
たとえば、k=1 のときは、25 =→ 32 個 です。
-
{ }
{ 1 } { 2 } { 3 } { 4 } { 5 }
{ 1, 2 } { 1, 3 } { 1, 4 } { 1, 5 } { 2, 3 } { 2, 4 } { 2, 5 } { 3, 4 } { 3, 5 } { 4, 5 }
{ 1, 2, 3 } { 1, 2, 4 } { 1, 2, 5 } { 1, 3, 4 } { 1, 3, 5 }
{ 1, 4, 5 } { 2, 3, 4 } { 2, 3, 5 } { 2, 4, 5 } { 3, 4, 5 }
{ 1, 2, 3, 4 } { 1, 2, 3, 5 } { 1, 2, 4, 5 } { 1, 3, 4, 5 } { 2, 3, 4, 5 }
{ 1, 2, 3, 4, 5 }

たとえば、k=1 のときは、8個です。
{ } { 5 } { 1, 4 } { 2, 3 } { 1, 4, 5 } { 2, 3, 5 } { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 }
k=1 のとき、答えを導く面白い方法があります。それは次の式を展開することです。
(1+x1)(1+x2)(1+x3)(1+x4)(1+x5)
展開すると次のようになります。
x0+x1+x2+2x3+2x4+3x5+3x6+3x7+3x8+3x9+3x10+2x11+2x12+x13+x14+x15
x の指数は要素の数の総和に相当し、係数はその要素の数の総和になっている部分集合の数に相当します。
そこで、x0 と x5 と x10 と x15 の係数の総和をとって、8となります。
これから、① の式を導いてみます。まず次のような関数を用意します。
f (x) = (1+x1)(1+x2)(1+x3)・・・(1+x5k-1)(1+x5k) ・・・ ②
次に、5乗すると1になる5つの複素数を考えます。それらを w1 から w5 とします。
w1 = e2π×(1/5) i w2 = e2π×(2/5) i w3 = e2π×(3/5) i w4 = e2π×(4/5) i w5 = e2π×(5/5) i
w1 から w5 は全て x に代入すると次の式を満たします。
x5-1 = (x-w1)(x-w2)(x-w3)(x-w4)(x-w5) = 0 ・・・ ③
また、次の式が成り立ちます。
w1+w2+w3+w4+w5 = 0
また、次の式たちが成り立ちます。
w12 = w2 w13 = w3 w14 = w4 w15 = w5
w22 = w4 w23 = w1 w24 = w3 w25 = w5
w32 = w1 w33 = w4 w34 = w2 w35 = w5
w42 = w3 w43 = w2 w44 = w1 w45 = w5
w52 = w5 w53 = w5 w54 = w5 w55 = w5
したがって、次の式たちが成り立ちます。
w12+w22+w32+w42+w52 =→ w1+w2+w3+w4+w5 = 0
w13+w23+w33+w43+w53 =→ w1+w2+w3+w4+w5 = 0
w14+w24+w34+w44+w54 =→ w1+w2+w3+w4+w5 = 0
w15+w25+w35+w45+w55 =→ 5 × w5 =→ 5 × 1 =→ 5
w16+w26+w36+w46+w56 =→ w15 × w1 + w25 × w2 + w35×w3 + w45 × w4 + w55 × w5
=→ w1+w2+w3+w4 + w5 = 0
式② に x=w1 を代入すると、
f (w1) = (1+w11)(1+w12)(1+w13)・・・(1+w15k-1)(1+w15k)
= c0+c1w11+c2w12+c3w13+c4w14+c5w15+c6w16+・・・・
同様にして、次の式たちが成り立ちます。
f (w2) = (1+w21)(1+w22)(1+w23)・・・(1+w25k-1)(1+w25k)
= c0+c1w21+c2w22+c3w22+c4w24+c5w25+c6w26+・・・・
f (w3) = (1+w31)(1+w32)(1+w33)・・・(1+w35k-1)(1+w35k)
= c0+c1w31+c2w32+c3w33+c4w34+c5w35+c6w36+・・・・
f (w4) = (1+w41)(1+w42)(1+w43)・・・(1+w45k-1)(1+w45k)
= c0+c1w41+c2w42+c3w42+c4w44+c5w45+c6w46+・・・・
f (w5) = (1+w51)(1+w52)(1+w53)・・・(1+w55k-1)(1+w55k)
= c0+c1w51+c2w52+c3w52+c4w54+c5w55+c6w56+・・・・
f (w1)+f (w2)+f (w3)+f (w4)+f (w5)
= 5c0 + c1 (w11+w21+w31+w41+w51)
+ c2 (w12+w22+w32+w42+w52)
+ c3 (w13+w23+w33+w43+w53)
+ c4 (w14+w24+w34+w44+w54)
+ c5 (w15+w25+w35+w45+w55)
+ c6 (w16+w26+w36+w46+w56)
+ ・・・・・
= 5c0 + 5c5 + 5c10 + 5c15 + ・・・・+ 5c5k(5k+1)/2 ・・・ ④
さて、③ の = 0 を削除した式に x=-1 を代入すると、
(-1)5-1 = (-1-w1)(-1-w2)(-1-w3)(-1-w4)(-1-w5) = 0
よって、
2 = (1+w1)(1+w2)(1+w3)(1+w4)(1+w5)
式② に x=w1 を代入すると、
f (w1) = (1+w11)(1+w12)(1+w13)・・・(1+w15k-1)(1+w15k)
= {(1+w1)(1+w2)(1+w3)(1+w4)(1+w5)}k
= 2k
同様にして、次の式たちが成り立ちます。
f (w2) = (1+w21)(1+w22)(1+w23)・・・(1+w25k-1)(1+w25k)
= {(1+w1)(1+w2)(1+w3)(1+w4)(1+w5)}k
= 2k
f (w3) = (1+w31)(1+w32)(1+w33)・・・(1+w35k-1)(1+w35k)
= {(1+w1)(1+w2)(1+w3)(1+w4)(1+w5)}k
= 2k
f (w4) = (1+w41)(1+w42)(1+w43)・・・(1+w45k-1)(1+w45k)
= {(1+w1)(1+w2)(1+w3)(1+w4)(1+w5)}k
= 2k
f (w5) = (1+w51)(1+w52)(1+w53)・・・(1+w55k-1)(1+w55k)
= (1+w5)5k
= 25k
f (w1)+f (w2)+f (w3)+f (w4)+f (w5) = 25k + 4×2k ・・・ ⑤
④ と ⑤ より、
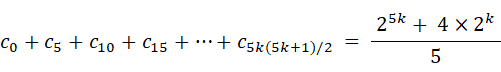
 数理論 へ戻る
数理論 へ戻る