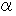地球の自転の角速度の大きさを とします。 すると、 北緯 度 の地点の地面の「 地軸を中心とする公転 」の角速度の大きさは になり、 北緯 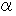度 の地点の地面の「 北極星を向く軸を中心とする自転 」の角速度の大きさは になります。 また、 北緯 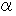度 の地点の地面の「 鉛直軸を中心とする水平面上での自転（ 垂直軸自転 ）」の角速度の大きさは 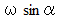になり、 北緯 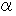度 の地点の地面の「 北向き水平軸を中心とする自転（ 水平軸軸自転 ）」の角速度の大きさは 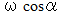になります。
　 さて、 フーコーの振り子を考える時に、 観察者は北緯 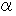度 の地面に立っていますので、 それが観察者の座標系になります。 それは、 角速度の大きさ 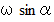の自転座標系です。 北緯 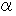度 の地面の南方向を 軸 の向き、東方向を 軸 の向きとします。 そしてフーコーの振り子をまず南北方向に振動させます。 観察者の座標系に対して角速度の大きさ 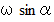で時計回りに回転している座標系が静止座標系になりますが、 その静止座標系において、 振り子の中心振動軸の投影を原点とし、 振り子が最大に振れた時（ 折り返し点 ）の重りの位置の１つの投影座標を 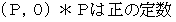とします。

　 ではこれから、「 等速自転座標系における質点の加速度 」の公式を用いて、 フーコーの振り子の軌道が回転することを証明します。 思考簡略化のため、フーコーの振り子の長さは振幅に比べて十分に長いものとし、振り子は等速折り返し運動をするものとします。 なお、「 等速自転座標系における質点の加速度 」につきましては、　力学 ＞ 等速自転座標系の運動方程式　をご覧ください。

　　　　

　　　　

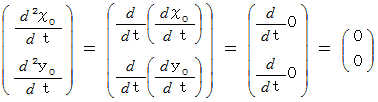
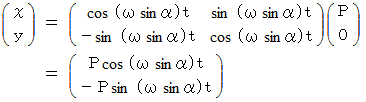
　 この式より、 振り子が最大に触れた時の折り返し点の重りの位置の投影は地面という等速自転座標系からすると、 反時計回りに角速度 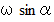の大きさで回転していることが解ります。 また、 この式より次の式が導かれます。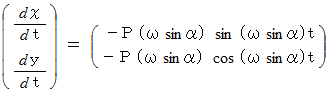

　　　　

よって、「 等速自転座標系における質点の加速度 」は次のようになります。

　　　　

　 この式の両辺に重りの質量をかけると運動方程式になります。 すると、 フーコーの振り子の回転の原因は 遠心力 と コリオリの力 とであることが解ったような気になります。 しかし、これは地球上の局所的微小地面が垂直軸等速自転をしているので、フーコーの振り子を局所的微小地面の観察者が観察すると、このようになるというだけのことです。フーコーの振り子の軌道の回転の原因の本質は「 振り子運動による姿勢制御 」です。振り子運動による姿勢制御は、部分的移動拘束を伴う慣性の法則によって形成されます。これは「 剛体の回転運動による姿勢制御（ ジャイロ効果 ） 」と共に大変に重要な概念であります。