力学 へ戻る（１） 等速自転座標系における質点の運動方程式
-
簡単にするために２次元空間で考えることにします。 思考実験につき、 観察者Ｂさん と 観察者Ａ君 は同じ位置にいるとします。 観察者Ａ君は、 観察者Ｂさんに対して、 一定の角速度
で反時計回りに自転しています。 これから観察者Ｂさんの立場になって考えます。 観察者Ａ君の座標系を「 等速自転座標系 」と言うことにして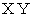 
で表します。 一方、 Ｂさんの座標系を「 静止座標系 」と言うことにして 
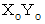で表します。等速自転座標系
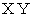において、 観察者Ａ君が観察者Ｂさんと同じ方向を向いた瞬間から 
の時間経過した瞬間です。 質量 
の質点Ｐ が座標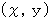 
の位置に存在しており、 加速度運動をしています。このとき、 質点Ｐ は静止座標系
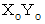ではどの位置に存在するのかを考えてみましょう。 この座標変換は、 同一座標系において 
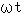の角度だけ反時計回りに回転させる座標変換と同じになりますので、 次のように表すことができます。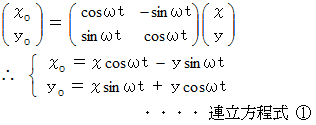
連立方程式
を で微分すると、 等速自転座標系の座標値を使って、 静止座標系における質点Ｐ の速度 
を表示することができます。
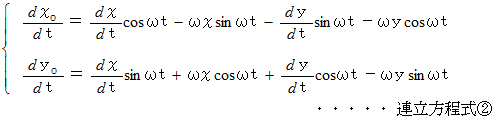
連立方程式
をさらに で微分すると、 等速自転座標系の座標値を使って、 静止座標系における質点Ｐ の加速度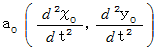 
を表示することができます。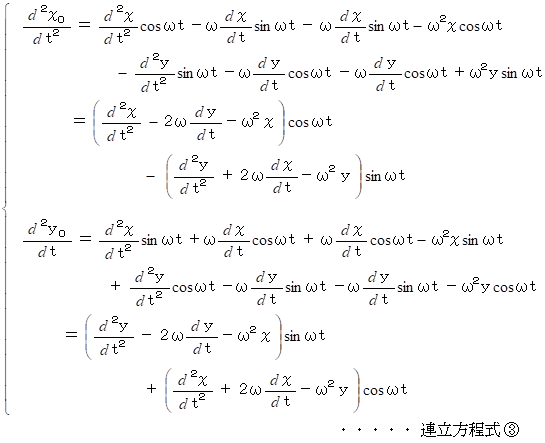
連立方程式
より、 次の式が成り立ちます。
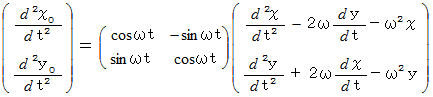
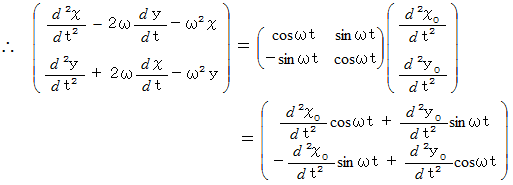
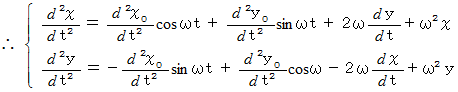
式
は、 一般的には、 ベクトルを使って次のように書かれます。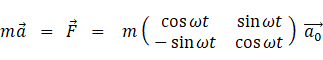
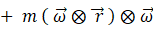
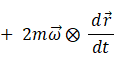
ただし、
____
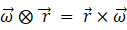
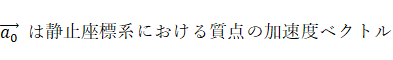
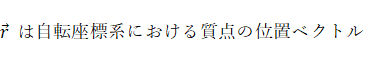
右辺の第１項は、 静止座標系における加速度ベクトルを等速自転座標系に座標変換したものに質量をかけたものです。 右辺の第１項は、 等速自転座標系における現実の力であり、 右辺の第２項は等速自転座標系における遠心力（ みかけの力 ）であり、 第３項は等速自転座標系におけるコリオリの力（ みかけの力 ）です。 この式を「 等速自転座標系における質点の運動方程式 」と私は言っています。