数理論 へ戻る
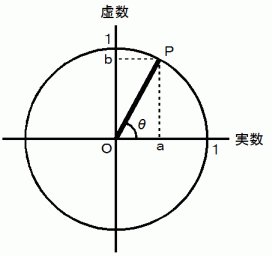
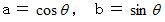
複素平面 では、 点
の位置は次のように表されます。
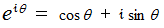
※ 参照： 大学生のための数学 ＞ 三角関数 指数・対数関数 ＞ おいらの愛した波動方程式
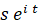という複素ベクトル（ 複素数 ）があり、次のような演算を考えます。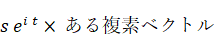
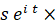という部分は、対象とする複素ベクトルを反時計回りに t ラジアン回転させてから大きさを s 倍にするという演算を意味します。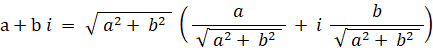
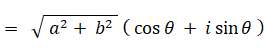
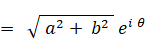
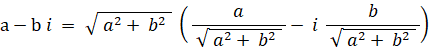
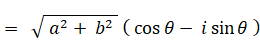
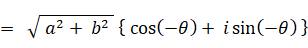
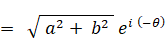
a + b i と a − b i とは互いに複素共役の関係にあります。共役複素数は、対になっている相手の複素ベクトル（ 複素数 ）に対して掛けるという演算をすると、それを実数軸の正の方向まで回転し、大きさを元の２乗にします。次のように、 a − b i に対して a + b i を掛けるという演算を行うと、a − b i は実数軸の正の方向まで回転して、大きさが元の２乗になります。
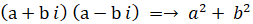
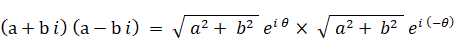
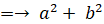
※ 参照： 大学生のための数学 ＞ 線形代数学 ＞ 第３のベクトルのかけ算