０ 〜 １ の実数を無作為に抽出するとき、 確率変数 x についての確率密度関数 ｆ(x) は ｆ(x) ＝ １ の連続一様分布をとります。
　 無数に抽出したとき、
　　　　母平均 ：　0.5000
　　　　母分散 ：　1 / 12　＝→　0.083333･･･
　　　　　　（ 参 考 ）
　　　　　　　　　
　　　　　　　　　　　　　　　　　

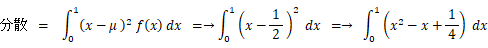
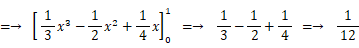
抽出する標本数により、 標本平均 や 標本分散 は 母平均 や 母分散 との差が異なります。
１万回シミュレーションしてみます。

標本数？ （ 10 〜 100 )　　　　　

標本平均の平均値 ：　
標本分散の平均値 ：　
標本不偏分散の平均値 ：　
修正標本分散（ 標本平均の代わりに母平均を用いて計算 ）の平均値 ：　

母分散に近いのは、 標本分散ではなくて、 標本不偏分散です。
その理由は、 標本分散を求めるのに、 母平均でなく、 標本平均を用いているからです。
標本平均を用いると、 どうしても標本分散は母分散よりも小さくなります。
標本数を N とすると、 標本分散 は 標本不偏分散 の N−1 / N 倍の大きさになります。
標本数が多くなれば、 標本分散 は 標本不偏分散 に近づきます。

プログラムの内容 ：