（４） 回転は２つの方向に分解することができる
-
フーコーの振り子のしくみを解明するために登場してきたのが、「 回転は２つの方向に分解することができる。」という考え方です。 地球内の各点は、 地軸に垂直な平面上を同じ角速度で回転しています。 そこで「 回転ベクトル 」を定義し、 地球内の各点には、 どこも同じ大きさで北を向いた「 回転ベクトル 」が存在しているとするのです。 そしてそれは合成・分解することができると考えるのです。 地球内の各点で共通する「 回転ベクトル 」の大きさを地球の自転の角速度
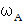で表すことにします。 すると、 地球内の各点に存在する普遍的な「 地球自転の回転ベクトル 」は、 大きさは 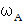で方向は北向きということになります。 たとえば、 北極点においては海面は水平面上（ 北極では、 水平面は赤道面と平行になります。）を北極点を中心にして角速度 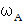で東に向かって回転していますが、 それを北極点を起点とする大きさ 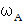で北向きの「 地球自転の回転ベクトル 」が表しているとします。 また、 赤道上の海面は水平面では全く回転していませんが、 角速度 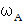で赤道面上を東に向かって回転しています。 これをその赤道上の点を起点とする大きさ 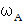で北向きの「 地球自転の回転ベクトル 」が表しているとします。 北緯45度の海上の点でも、 海面は、 赤道面と水平な平面上を角速度 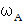で東へ向かって回転しており、 そのことを、 大きさ 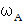で北向きの「 地球自転の回転ベクトル が表しているのですが、 それを、 北緯４５度の海上の水平面上の北向きと鉛直方向に２分解すると、 それぞれ大きさが 
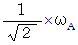のベクトルになりますので、 北緯45度の海上の点では、 海面は、 角速度 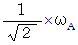で水平面を回転しながら、 角速度 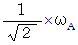で赤道面と45度の傾きで交わる面上を回転していると言っても良いことになります。 この２つの回転を合成すると、 赤道面と水平な方向に角速度 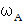で東へ向かって回転していることになります。この「 回転の合成 」を実感するには、 聴診器または硬めのコードが必要です。 聴診器の両側を左右の手で握ります。 左手は掌が顔を向くように右手は手背が顔を向くように握ります。 そして、 聴診器を中央が直角カーブになるように折ります。 用意が出来たら、 頂部を形成した 約 10 cm の聴診器の中央を見ながら、 両手を同時に反時計方向に捻じります。 すると聴診器は α ループを形成しますが、 頂部の直線の動きをよく見てください。 それは水平面を反時計方向に180度回転しています。 これが回転の合成によってできた回転です。
さて、 地球内部の点と違って、 振り子には、 その振動の原因となる一様な重力場と反対方向の「 回転ベクトル 」の大きさは０であり、 振り子の支柱にそのような回転ベクトルを与えたとしても、 その方向への「 回転ベクトル 」は重りには伝わりません。 それは振り子の重りには水平方向には全く力が作用しないからです。 したがって、 一様な重力場と平行な方向から振り子運動を観察している人にとっては、 振り子はその軌道を変えません。 振り子が存在する点に「 地球自転の回転ベクトル 」が加わっているとき、 水平方向と鉛直方向に分解された回転ベクトルは、 海面円盤と振り子とで次のように異なっています。
|
|
海面円盤 |
振り子 |
||
|
水平方向 |
鉛直方向 |
水平方向 |
鉛直方向 |
|
|
北極点 |
０ |
|
０ |
０ |
|
北緯45度 |
|
|
|
０
|
|
赤道上 |
|
０ |
|
０ |
鉛直方向を向いている「 回転ベクトル 」は水平方向の回転を表します。 したがって、 振り子は水平方向には回転しないけれど、 海面円盤は水平方向に回転します。 そのために、 相対的に振り子が水平方向に回転していることになります。 これがフーコーの振り子の原理だったのです。 なお、 鉛直方向への回転は、 海面円盤も振り子も同じですから、 振り子は、 鉛直方向へは相対的に回転していないことになります。 この水平方向と鉛直方向への回転の分割こそ、 フーコーの振り子の式の中の
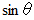なのです。-
フーコーの振り子は、 既存の理論では説明できないので、 それを裏付ける新しい理論の発見が必要だったのです。 フーコーの実験直後に上記のような考えを発表した人がいます。 リューヴィルという人です。 彼の考えには「 角速度 」という概念はありませんでしたが、 その発想法の斬新さは十分に受け入れられたようです。 しかし、 残念ながらフーコーの振り子の原理としては受け入れられなかったようです。 当時からすれば当然のことだと思います。 しかし、 この発想が新しい理論に繋がったのです。 リューヴィルが思いついたのは、 剛体の回転運動 や 天体の回転運動理論 の中で登場する「 角速度ベクトルの合成・分解 」そのものなのですから。 したがって、 上記の「 回転ベクトル 」という言葉は「 角速度ベクトル 」という言葉にそっくりそのまま置き換えることができます。
論文の最初へ戻る