実数または虚数のみでなるガウス整数は、 その大きさが 4 で割ると 3 余る素数で表されるものがガウス素数であり、 実数と虚数の両方からなるガウス整数
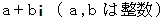 は、 ノルム ( 大きさの2乗 :
は、 ノルム ( 大きさの2乗 : 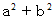 ) が素数であるものがガウス素数です。
) が素数であるものがガウス素数です。 ガウス整数
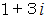 を素因数分解してみましょう。 ( ガウス素数の積の形に変形してみましょう。)
を素因数分解してみましょう。 ( ガウス素数の積の形に変形してみましょう。)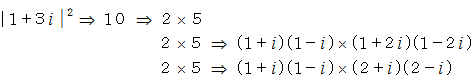
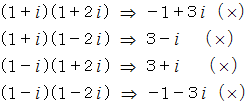
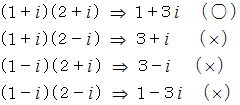
したがって、
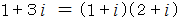 です。
です。続いて、 ガウス整数
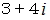 を素因数分解してみましょう。
を素因数分解してみましょう。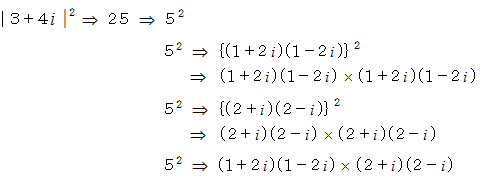
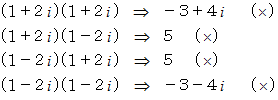
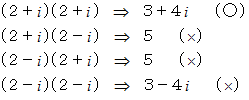
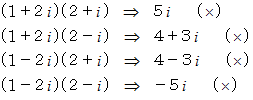
したがって、
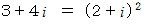 です。
です。最後に、 ガウス整数 14 を素因数分解してみましょう。
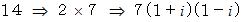 です。
です。 数理論 へ戻る
数理論 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る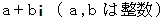 は、 ノルム ( 大きさの2乗 :
は、 ノルム ( 大きさの2乗 : 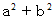 ) が素数であるものがガウス素数です。
) が素数であるものがガウス素数です。 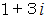 を素因数分解してみましょう。 ( ガウス素数の積の形に変形してみましょう。)
を素因数分解してみましょう。 ( ガウス素数の積の形に変形してみましょう。)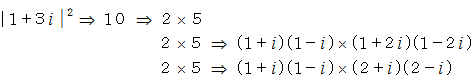
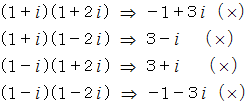
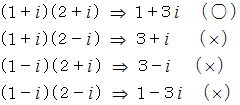
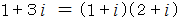 です。
です。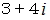 を素因数分解してみましょう。
を素因数分解してみましょう。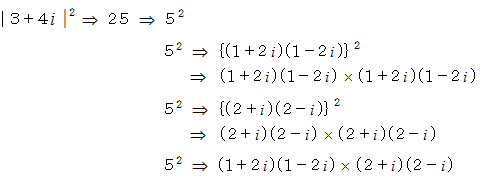
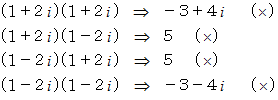
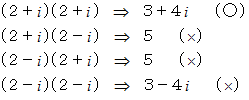
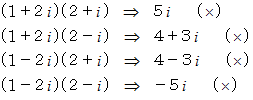
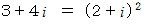 です。
です。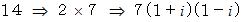 です。
です。