全体集合を、 ガウス整数とします。
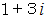 の約数を探してみましょう。
の約数を探してみましょう。  と
と 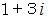 は自明です。 それ以外のものを探します。
は自明です。 それ以外のものを探します。まず、
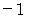 はどうでしょうか。
はどうでしょうか。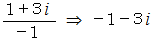
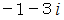 は全体集合の要素です。 したがって、
は全体集合の要素です。 したがって、 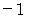 と
と 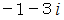 は
は 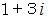 の約数であることが解りました。
の約数であることが解りました。次に、
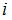 はどうでしょうか。
はどうでしょうか。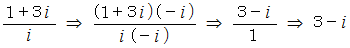
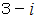 は全体集合の要素です。 したがって、
は全体集合の要素です。 したがって、 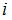 と
と 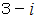 は
は 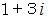 の約数であることが解りました。
の約数であることが解りました。次に、
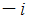 はどうでしょうか。
はどうでしょうか。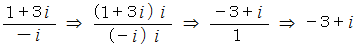
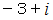 は全体集合の要素です。 したがって、
は全体集合の要素です。 したがって、 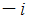 と
と 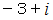 は
は 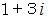 の約数であることがわかりました。
の約数であることがわかりました。次に、
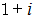 はどうでしょうか。
はどうでしょうか。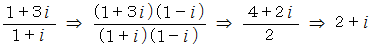
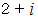 は全体集合の要素です。 したがって、
は全体集合の要素です。 したがって、 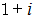 と
と 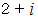 は
は 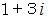 の約数であることが解りました。
の約数であることが解りました。次に、
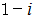 はどうでしょうか。
はどうでしょうか。
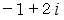 は全体集合の要素です。 したがって、
は全体集合の要素です。 したがって、 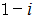 と
と 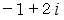 は
は 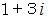 の約数であることが解りました。
の約数であることが解りました。次に、
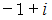 はどうでしょうか。
はどうでしょうか。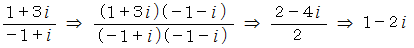
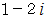 は全体集合の要素です。 したがって、
は全体集合の要素です。 したがって、 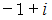 と
と 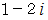 は
は 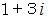 の約数であることが解りました。
の約数であることが解りました。次に、
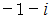 はどうでしょうか。
はどうでしょうか。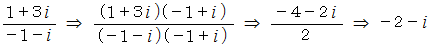
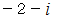 は全体集合の要素です。 したがって、
は全体集合の要素です。 したがって、 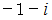 と
と 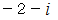 は
は 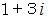 の約数であることが解りました。
の約数であることが解りました。次に、
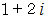 はどうでしょうか。
はどうでしょうか。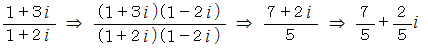
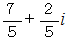 は全体集合の要素ではありません。 したがって、
は全体集合の要素ではありません。 したがって、 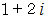 は
は 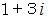 の約数ではありません。
の約数ではありません。次に、
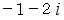 はどうでしょうか。
はどうでしょうか。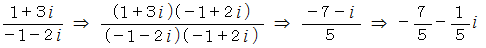
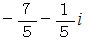 は全体集合の要素ではありません。 したがって、
は全体集合の要素ではありません。 したがって、 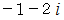 は
は 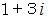 の約数ではありません。
の約数ではありません。同様にして、
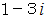 、
、 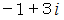 、
、 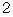 、
、 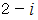 、
、 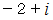 、
、 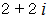 、
、 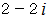 、
、 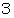 、
、 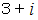 、
、 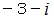 を見ていきますと、 これらはすべて
を見ていきますと、 これらはすべて 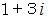 の約数ではないことが解ります。
の約数ではないことが解ります。最後に、 ノルムが
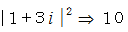 を超えるガウス整数で
を超えるガウス整数で 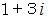 を割っても、
を割っても、  余り ○ ○ の形になります。
余り ○ ○ の形になります。したがって、
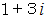 の約数は次の16個になります。
の約数は次の16個になります。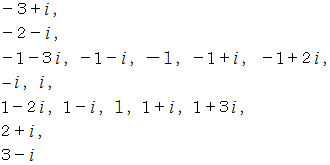
このように、 すべての約数を見つけるのは大変ですので、 次のような十進BASIC のプログラムを実行すれば、 簡単に見つけることができます。
 数理論 へ戻る
数理論 へ戻る