【 問 題 】

　10月10日23時59分59.9999999・・・秒 は、10月10日ではないことを証明せよ。

【 証 明 １ 】

59.99999999999・・・　＝　59 ＋ 0.99999999999・・・　である。
a　＝　0.99999999999・・・・　とおくと、
　　　　　10 a − a　＝　9
　　　　　したがって、　a　＝　１
ということは、 59.99999999999・・・ ＝ 59 ＋ 0.99999999999・・・ ＝ 59 ＋ 1 ＝ 60　である。
ということは、 10月10日23時59分59.9999999・・・秒　＝　10月11日0時0分0秒 　である。
ということは、 10月10日23時59分59.9999999・・・秒 は 10月11日 である。
ということは、 10月10日23時59分59.9999999・・・秒 は 10月10日 ではない。

【 証 明 ２ 】

1/3　＝　0.33333333333・・・・
2/3　＝　0.66666666666・・・・
１　＝　1/3 ＋ 2/3　＝　0.99999999999・・・・

1/7　＝　0.142857142857・・・・
6/7　＝　0.857142857142・・・・
１　＝　1/7 ＋ 6/7　＝　0.99999999999・・・・
　　　　　　　　　　　　　　　　　　　（ このあと略 ）

【 証 明 ３ 】

a　＝　0.9 ＋ 0.09 ＋ 0.009 ＋ 0.0009 ＋ ・ ・ ・ ・　とおくと、
初項 0.9、 公比 0.1 の等比無限数列の和より、 次のようになる
　　　　　
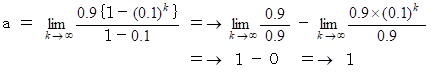
　　　　　　　　　　　　　　　　　　　（ このあと略 ）

【 結 論 】

　 したがって、 0.99999999999・・・・　は １よりも小さくて限りになく１に近い数ではないのだ。
　 では、１よりも小さくて限りになく１に近い数は？　１−1/∞ ？
　 また、０よりも大きくて限りになく０に近い数は？　1/∞ ？