【 問 題 １ 】

　 保健の仕事に携わっている人の集合をＡ、 治療の仕事に携わっている人の集合をＢ、 福祉の仕事に携わっている人の集合をＣ とします。 500人に聞いたところ、 次のような結果でした。
　　　　　

　　　　　Ａ： 40人　　　Ｂ： 36人　　　Ｃ： 34人
　　　　　Ａ かつ Ｂ： 10人　　　Ｂ かつ Ｃ： 12人　　　Ｃ かつ Ａ ： 18人
　　　　　Ａ かつ Ｂ かつ Ｃ ： 5人

　 この３つの仕事のどれにも携わっていない人は何人だったしょうか？　Ａ かつ Ｂ かつ Ｃ の人は、 Ａ かつ Ｂ に含まれますし、 また Ａ にも含まれていることに気をつけて解答してください。

【 解 答 】

　 500 − { ( 40＋36＋34 ) − ( 10＋12＋18 ) ＋ 5 }　＝→　425 (人)

　 この式がピンとこない人は、 次のようにひとつづつ順番に数字を埋め込んでいっても解けますね。
　　　　　　　　　　　　　　

【 問 題 ２ 】

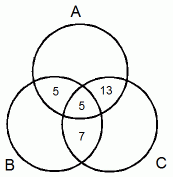
全体集合を1000以下の自然数とする。2 または 3 または 5 の倍数である自然数は何個あるか？

【 解 答 】

2 かつ 3 の倍数 ＝ 6 の倍数
3 かつ 5 の倍数 ＝ 15 の倍数
5 かつ 2 の倍数 ＝ 10 の倍数
2 かつ 3 かつ 5 の倍数 ＝ 30 の倍数

2 の倍数の個数：
　　1000÷2 の 商 ＝ 500
3 の倍数の個数：
　　1000÷3 の 商 ＝ 333
5 の倍数の個数：
　　1000÷5 の 商 ＝ 200
6 の倍数の個数：
　　1000÷6 の 商 ＝ 166
15 の倍数の個数：
　　1000÷15 の 商 ＝ 66
10 の倍数の個数：
　　1000÷10 の 商 ＝ 100
30 の倍数の個数：
　　1000÷30 の 商 ＝ 33

( 500+333+200 ) − ( 166+66+100 ) + 33　＝→　734 (個)