【 問 題 】

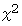「 が奇数ならば、 は奇数である。」という命題が真であることを証明せよ。

【 解 答 】

この包含命題の前提命題 ：
　　「 は、 ２乗すると奇数になる数で構成される集合の要素である。」
この包含命題の結論命題 ：
　　「 は、 奇数の集合の要素である。」

　「２乗すると奇数になる数で構成される集合 」が「 奇数の集合 」の部分集合であることを明らかにすればいいのだが、 困難なような気がする。 そこで対偶命題を作り、 それが真の包含命題であることを証明することにする。

対偶命題 ：
　　「 が偶数ならば、 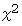は偶数である。」

は偶数なので、 次のように表すことができる。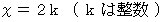
　　　
　 すると、 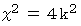となり、 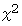が偶数であることがわかる。 したがって、 この対偶命題は真であることがわかった。 したがって、 この命題は真であることがわかった。

【 解 説 】

　 三段論法による「 包含命題 」の説明のガイドラインはこうです。「 それは Ａ の要素である。 Ａ は Ｂ の部分集合である。 したがって、 それは Ｂ の要素である。」

　　　　　

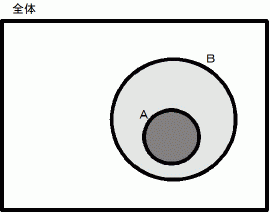
　 対偶法は、 Ａ の補集合を Ａ’とし、 Ｂ の補集合を Ｂ’とします。 そして、 Ｂ’は Ａ’の部分集合であることを明らかにした後で、 三段論法を使います。「 あれは、 Ｂ’の要素である。 Ｂ’は Ａ’の部分集合である。 したがって、 あれは Ａ’の要素である。」対偶命題が真であることが証明されると、 元の命題が証明されたことになります。

　 命題の証明をする場合、 包含命題の前提命題は真です。 つまり、「 これは集合Ａ に属します。」です。 また、 包含命題の結論命題も真です。 つまり、「 これは集合Ｂ に属します。」です。 命題の証明は、「 集合Ａ は集合Ｂ の部分集合である。」ことを明らかにすることです。 しかし、 そうすることが困難な場合があります。 そこで、 対偶命題を作ってそれを証明するのが対偶法です。 対偶命題の前提命題は真です。 つまり、「 それは集合 NOT-Ｂ に属します。」です。 また、 対偶命題の結論命題も真です。 つまり、「 それは集合 NOT-Ａ に属します。」です。 対偶命題の証明は、「 集合 NOT-Ｂ は集合 NOT-Ａ の部分集合である。」ことを明らかにすることです。

　　　包含命題 （ 集合Ａ が 集合Ｂ に含まれる場合 ） の 真偽表

　　　　　Ａ　Ｂ　 　NA　 NB　　 NB→NA　 A→B
　　　　============================
　　　　　1　 1　　　0　　0　　　　0　　　　1
　　　　　1　 0　　　0　　1　　　　0　　　　0
　　　　　0　 1　　　1　　0　　　　0　　　　0
　　　　　0　 0　　　1　　1　　　　1　　　　0

　　　　　　　　1 ：　真　　（ は 集合Ａ に属する。）　（ 命題は正しい。）
　　　　　　　　0 ：　偽　　（ は 集合Ａ に属さない。）　（ 命題は正しくない。）
　　　　　　　　A → B ：　命題　（ Ａ ならば Ｂ である。）
　　　　　　　　NB → NA ：　対偶命題　（ Ｂでない ならば Ａでない。）