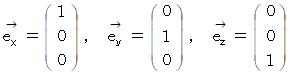
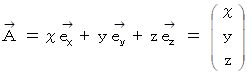
3次元基底ベクトルのベクトリオ 6種類 * ベクトリオは私の造語です。
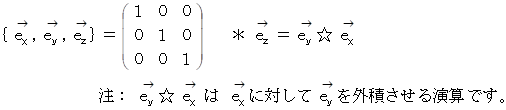
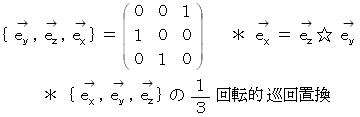
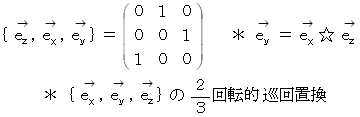
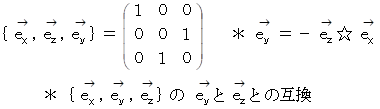
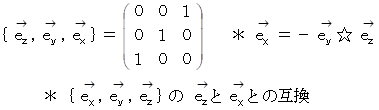
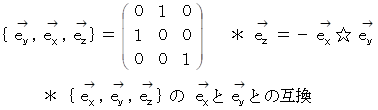
これら6つのベクトリオは、 すべて直交行列です。 直交行列は、 互いに直交する大きさが 1 のベクトルたちによる順列の表現行列が正方行列になっており、 その逆行列はその転置行列に一致しています。
(1) 座標変換の視点で捉える6つのベクトリオ

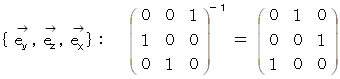
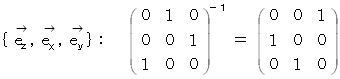


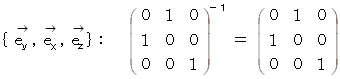
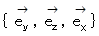 と
と  の表現行列の逆行列は、 その表現行列の転置行列になっていて、 その表現行列と一致してはいません。 一方、 それ以外のベクトリオの表現行列の逆行列は、 その表現行列の転置行列になっていて、 かつ、 その表現行列と一致しています。
の表現行列の逆行列は、 その表現行列の転置行列になっていて、 その表現行列と一致してはいません。 一方、 それ以外のベクトリオの表現行列の逆行列は、 その表現行列の転置行列になっていて、 かつ、 その表現行列と一致しています。次のように、 6つのベクトリオの逆行列はそれぞれに、 ベクトルの座標変換を行う座標変換テンソルになっています。
1.
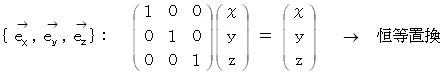
2.
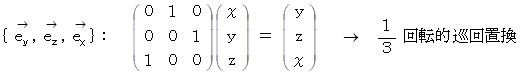
3.
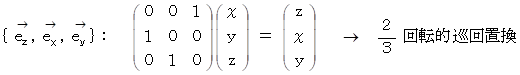
4.

5.
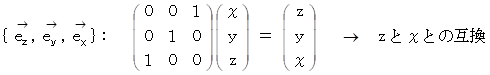
6.
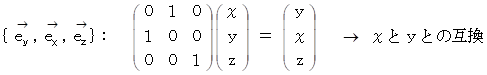
(2) 群の視点で捉える6つのベクトリオの逆行列
群の乗積表 : * 第1行の第2列〜第7列は かけられる行列、 第2行〜第7行の第1列は かける行列
 |
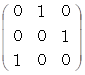 |
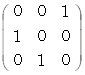 |
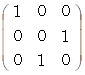 |
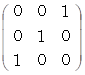 |
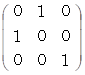 |
|
 |
 |
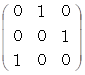 |
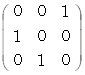 |
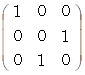 |
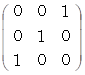 |
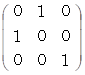 |
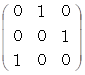 |
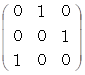 |
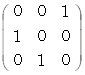 |
 |
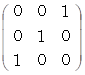 |
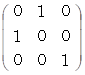 |
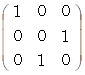 |
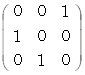 |
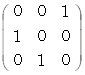 |
 |
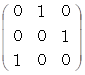 |
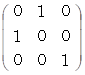 |
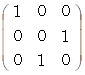 |
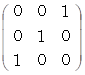 |
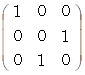 |
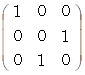 |
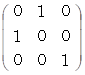 |
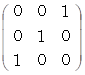 |
 |
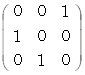 |
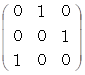 |
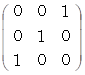 |
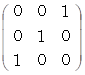 |
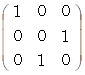 |
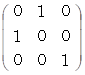 |
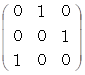 |
 |
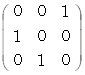 |
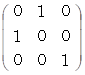 |
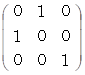 |
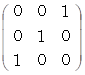 |
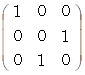 |
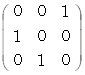 |
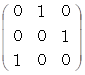 |
 |
-
1 は単位元です。 2の逆元は3で、 3の逆元は2です。
|
◇ |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
|
2 |
2 |
3 |
1 |
5 |
6 |
4 |
|
3 |
3 |
1 |
2 |
6 |
4 |
5 |
|
4 |
4 |
6 |
5 |
1 |
3 |
2 |
|
5 |
5 |
4 |
6 |
2 |
1 |
3 |
|
6 |
6 |
5 |
4 |
3 |
2 |
1 |
結合法則は成り立っているか? 確かめてみましょう。
( 例 )
4 ◇ 3 ◇ 2 =→ 4 ◇ 1 =→ 4
( 4 ◇ 3 ) ◇ 2 =→ 5 ◇ 2 =→ 4
5 ◇ 2 ◇ 6 =→ 5 ◇ 4 =→ 2
( 5 ◇ 2 ) ◇ 6 =→ 4 ◇ 6 =→ 2
ある集合に関して、 次の4つが言えるとき、 この集合を 群 と言う。
逆元とは、 ある要素が演算をする側に回り自分が演算をされる側に回ったとき、 その演算結果が単位元になり、 かつ、 その要素が演算をされる側に回り自分が演算をする側に回ったとき、その演算結果が単位元になる要素のことである。
群 では、集合の要素が数や物質など以外に演算子も含まれます。
-
1. 集合の要素の間にある演算が成り立ち、 その演算に関して集合は閉じている。
2. その演算( ◎ )に対して、 結合則が成り立つ。
* 結合則とは、a ◎( b ◎ c )= ( a ◎ b ) ◎ c
3. その演算に単位元が存在する。
4. その演算に逆元が存在する。
逆元とは、 ある要素が演算をする側に回り自分が演算をされる側に回ったとき、 その演算結果が単位元になり、 かつ、 その要素が演算をされる側に回り自分が演算をする側に回ったとき、その演算結果が単位元になる要素のことである。
群 では、集合の要素が数や物質など以外に演算子も含まれます。
 その他の数学 へ戻る
その他の数学 へ戻る