図A
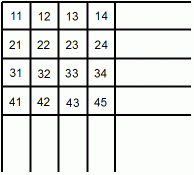
図A を見てください。 m 行目 n 列目 のマスの中には次の式で表される自然数が収まっています。
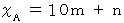
これを時計回りに45度回転します。 これを図A’ とします。
図A’
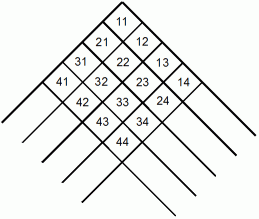
次に、 図A’ のマスの中の数字を次のように書き換えます。 これを図B’ とします。
図B’
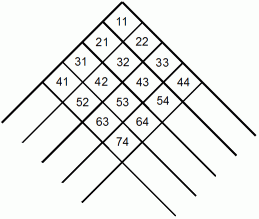
その次に、 これを反時計周りに45度回転します。 これを図B とします。
図B
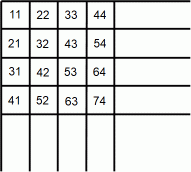
では、 問題です。 m 行目 n 列目 のマスの中には、 どんな数が収まっているでしょうか?
答えは、 10 m + 11 n − 10 です。
列ごとに数列を見てみましょう。 n 列目 の数列は、 初項 11 n 公差 10 の 等比数列です。 ですから、 その m 項目の数は次のようになります。
11 n + 10 ( m − 1 ) =→ 10 m + 11 n − 10
図B’ のマスの中の数字を次のように書き換えます。 これを図C’ とします。
図C’
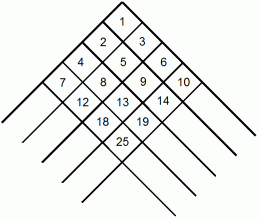
その次に、 これを反時計周りに45度回転します。 これを図C とします。
図C
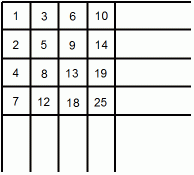
では、 問題です。 m 行目 n 列目 のマスの中には、 どんな数が収まっているでしょうか?
列ごとに数列を見てみましょう。 n 列目 の数列は、 階差数列が、 初項 n 公差 1 の 等比数列になっています。 ということは、 n 列目 の数列の k項目の数 ( ak ) と ( k−1 )項目の数 ( ak−1 ) との差は、 n + k − 1 になっています。 つまり、 次の式が成り立ちます。
ak−1 − ak = k + n − 1
a2 − a1 = 1 + n − 1
a3 − a2 = 2 + n − 1
a4 − a3 = 3 + n − 1
・
・
・
am − am−1 = m−1 + n − 1
上記の式たちを辺々足すと、
am − a1 = m ( m − 1 ) / 2 + ( n − 1 )( m − 1 )
n 列目 の数列の初項を求めましょう。 1 行目の数列は、 階差数列が 初項 2 公差 1 の等比数列になっています。 ということは、 1 行目の数列について次の式が成り立ちます。
ak−1 − ak = k + 2 − 1
a2 − a1 = 1 + 1
a3 − a2 = 2 + 1
a4 − a3 = 3 + 1
・
・
・
an − an−1 = n−1 + 1
上記の式たちを辺々足すと、
an − a1 = n( n − 1 )/ 2 + n − 1
よって、 am = n( n − 1 )/ 2 + n
したがって、 n 列目 の数列の初項は n( n − 1 )/ 2 + n になります。
したがって、 n 列目 の数列の m 項目の数は、 次の式で与えられます。
n( n − 1 )/ 2 + n + m( m − 1 )/ 2 +( n − 1 )( m − 1 )
=→ ( m2 + n2 + 2mn − 3m − n + 2 ) ÷ 2
別解の答えは次のようになります。
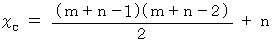
これは、 図A’ と 図C’ の数字を対応させることによって導かれたものです。 まず、 図C’の 1 列目 ( 図C の 1 列目と同じです。) のみに注目します。 1 行目 から m 行目 まで のマスの中の数を数列にしてみます。
1 2 4 7 11 ・ ・ ・
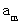
この階差数列の漸化式は次のように表されます。

したがって、 1 列目 の m 行目 のマスの中の数
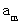 は次のようになります。
は次のようになります。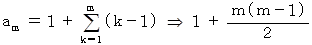
図A’ の 数
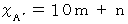 に対応する数字は、図C’ の
に対応する数字は、図C’ の 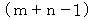 行目の n 列目 ( 図C の n 列目とは異なります。) のマスの中の数字です。 その数は次のように表されます。
行目の n 列目 ( 図C の n 列目とは異なります。) のマスの中の数字です。 その数は次のように表されます。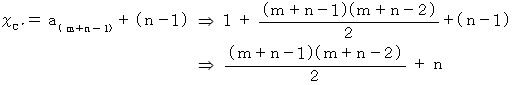
図A’ と 図C’ の数字の対応は、 図A と 図C の数字の対応と同じですから、 答えは次のようになります。
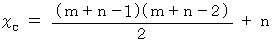
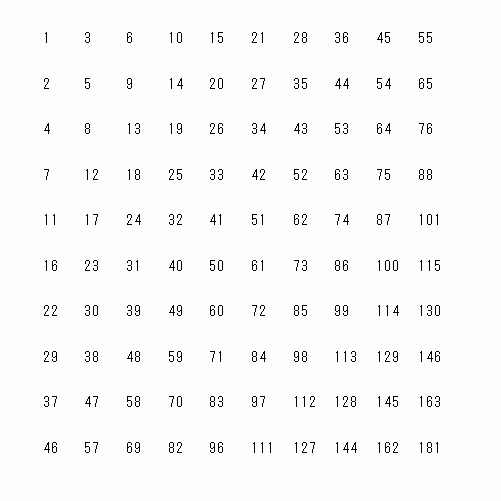
-
SET WINDOW 0,12,-1,10
FOR m=1 TO 10
FOR n=1 TO 10
LET i = (m^2+n^2+2*m*n-3*m-n+2)/2
PLOT TEXT ,AT n,10-m: STR$(i)
NEXT n
NEXT m
END
 数理論 へ戻る
数理論 へ戻る