図Ｂを描くための 十進BASIC のプログラム ：

　LET mmax = 10
　LET nmax = 10
　SET WINDOW −0.5, nmax+1.5, −1, mmax+0.5
　FOR m=1 TO mmax
　　FOR n=1 TO nmax
　　　LET mn = 10*(m−1) + n
　　　PLOT TEXT ,AT n, mmax−m: STR$(mn)
　　NEXT n
　NEXT m
　END

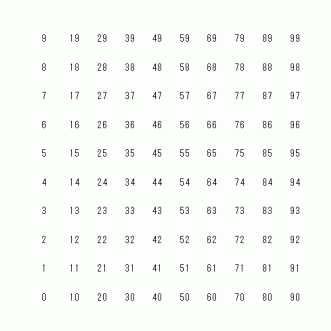
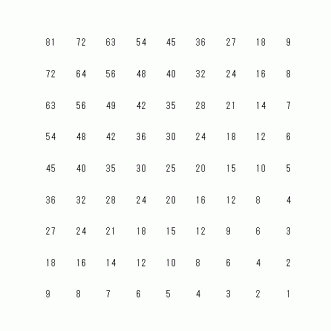
　 なぜそうなるのでしょうか？
　 列ごとに数列を見てみましょう。 n 列目 の数列は、 初項 a₁　公差 −1 の 等比数列になっています。
　 したがって、 n 列目 の数列の第 m 項は　a₁ − ( m − 1 )　になります。
　 n 列目 の初項 a₁ は、 １ 行目の数列の 第 n 項です。 １ 行目の数列は、 初項 9 公差 10 の等差数列ですから、 １ 行目の数列の 第 n 項は次の式で表されます。
　　　　9 + 10 × ( n −1 )
　 したがって、 n 列目 の数列の第 m 項は次の式で与えられます。
　　　　9 + 10 × ( n −1 ) − ( m − 1 )　＝→　−m + 10 × n

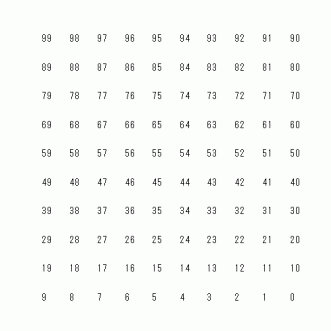
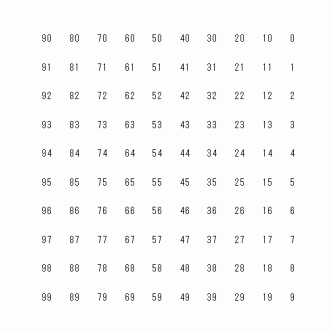
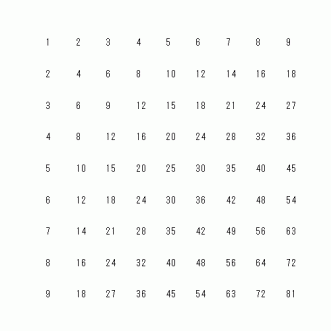
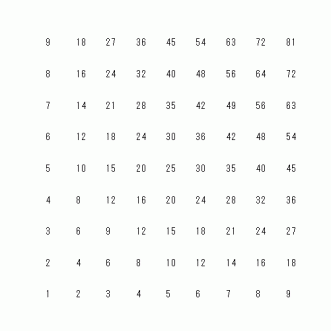
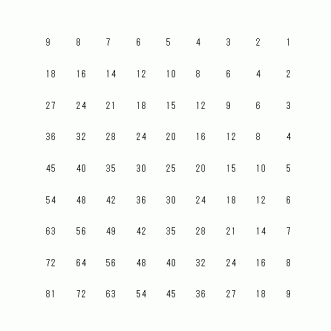
　 なぜそうなるのでしょうか？
　 列ごとに数列を見てみましょう。 n 列目 の数列は、 初項 a₁　公差 −n の 等比数列になっています。
　 したがって、 n 列目 の数列の第 m 項は　a₁ − n ( m − 1 )　になります。
　 n 列目 の初項 a₁ は、 １ 行目の数列の 第 n 項です。 １ 行目の数列は、 初項 9 公差 9 の等差数列ですから、 １ 行目の数列の 第 n 項は次の式で表されます。
　　　　9 + 9 × ( n −1 )
　 したがって、 n 列目 の数列の第 m 項は次の式で与えられます。
　　　　9 + 9 × ( n −1 ) − n ( m − 1 )　＝→　 ( 10 − m ) × n