（１）３角形を直線で３つに分割し、３ピースを組み合わせて長方形を作る。

　　　

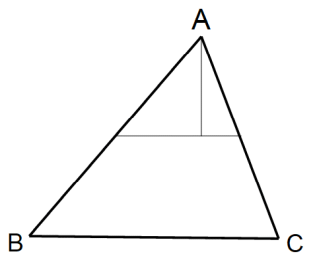
まず、辺ＡＢの中点と辺ＡＣの中点とを直線で結びます。
次に、点Ａから上記の線分に垂線を引きます。
そして、この２つの線分にハサミを入れ、３ピースに分割します。
そして、この３ピースを組み合わせて、一辺の長さがＢＣの長方形を作ります。

（２）２つの正方形を一方は直線で３つに分割し、もう一方は直線で２つに分割し、
　　５ピースを組み合わせて正方形を作る。

　　　
　　　　　　　　　　※ ２つの正方形が合同なときは、４ピースになります。

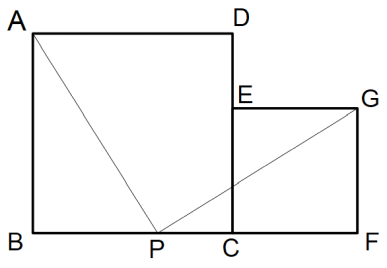
まず、２つの正方形を左から大きい順に横に並べてくっつけます。
次に、辺ＢＣ上に ＢＰ ＝ ＥＣ となるような点Ｐを取ります。
そして、点Ａと点Ｐを直線で結び、点Ｇと点Ｐを直線で結びます。
そして、この２つの線分にハサミを入れ、５ピースに分割します。
そして、この５ピースを組み合わせて、一辺の長さが root ( ＡＢ² ＋ ＥＣ² ) の長方形を作ります。
具体的には、まず、△ＡＢＰを点Ａを中心に回転させて、ＡＢをＡＤに合わせます。
次に、△ＧＰＦを点Ｇを中心に回転させて、ＦＧをＥＧに合わせます。

（３）長方形を直線で３つに分割し、３ピースを組み合わせて正方形を作る。

　　　

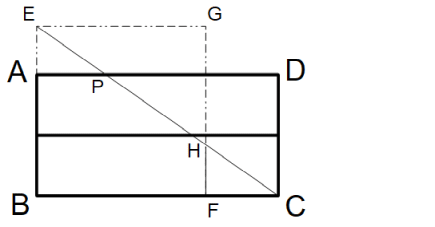
まず、長方形が横長の場合、何等分かして上にくっつけて並べ、正方形に比較的近い長方形にします。
　　　　（ 図は２等分してから上にくっつけて並べてます。）
次に、一辺の長さが root ( ＡＢ × ＢＣ ) の正方形ＥＢＦＧを作図します。
そして、点Ｅと点Ｃを直線で結びます。
そして、その線分のＡＤとの交点を点Ｐとし、線分ＧＦとの交点を点Ｈとします。
そして、線分ＰＣと線分ＨＦにハサミを入れ、３ピースに分割します。
そして、△ＨＦＣを△ＥＡＰに重ね、△ＰＣＤを△ＥＨＧに重ねます。
すると、正方形ＥＢＦＧができます。

（４）「ボヤイの定理」

　直線分だけで作られるすべての平面図形は３角形に分割できるので、以上の３つの方法を組み合わせれば、どんな図形でもハサミ分割して組み替えれば、正方形を作ることができます。
　ということは、直線分だけで作られるすべての平面図形は、ハサミ分割して組み替えれば、それと同じ面積の正方形を作ることができるので、直線分だけで作られるすべての平面図形は、ハサミ分割して組み替えれば、それと同じ面積のどんな図形でも作ることができるということです。これを「ボヤイの定理」と言います。