(1) 平方数の数列
-
次のような平方数の和の公式があります。
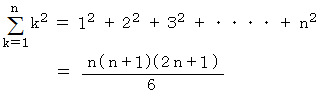
( 証明 その1 )
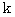 についての恒等式 :
についての恒等式 : 
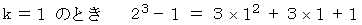

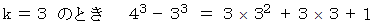
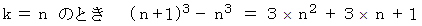
これらを辺々加えると、
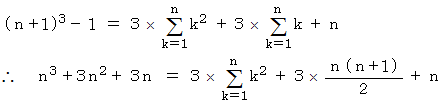
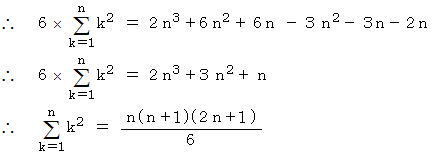
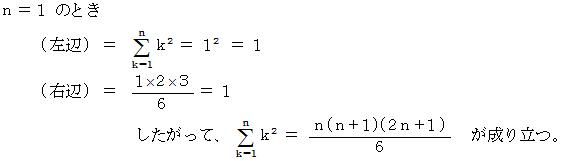


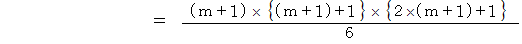
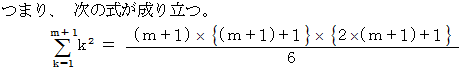
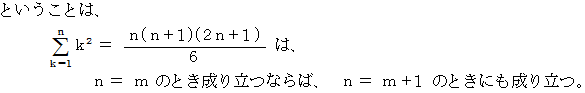
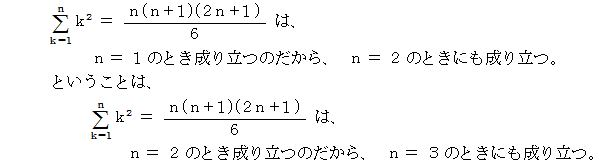
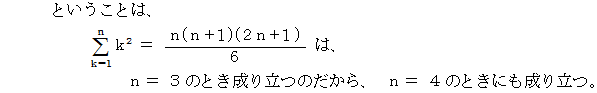

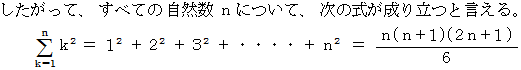
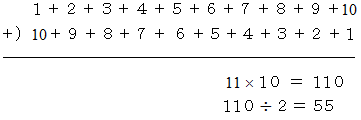
一般に、 1 から
 までの自然数の和は次のように表されます。
までの自然数の和は次のように表されます。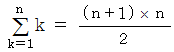
( 証明 )
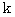 についての恒等式 :
についての恒等式 : 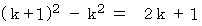

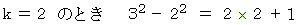
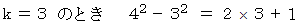
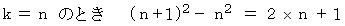
これらを辺々加えると、
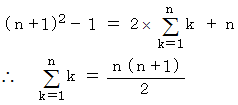
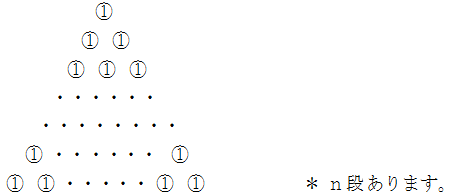

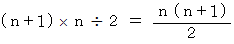
これを応用すると、 さきほどの平方数の和の公式を証明することができます。
まず、 次のような数字のピラミッドを作ります。
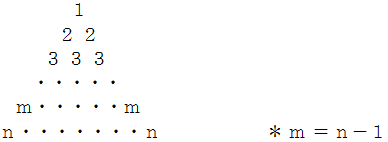
この数字のピラミッドを反時計回りに120度回転させます。
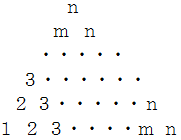
この数字のピラミッドを左右反転させて鏡面像を作ります。 ただし、 数字の文字は鏡面像にしていません。
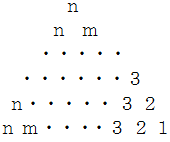
以上の3つの数字のピラミッドを重ねて、 重なる数字を加えると、
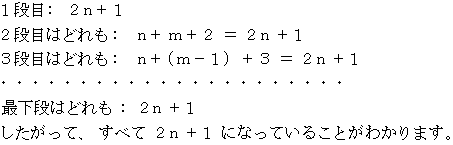
1つの数字のピラミッドに含まれる数字の個数は次のようになります。
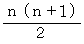
したがって、 数字のピラミッドに含まれる数の合計は次のようになります。
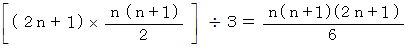
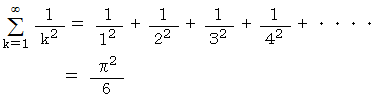
( 証明 )
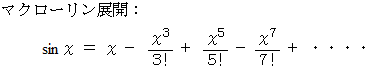
したがって、 次の式が成り立ちます。
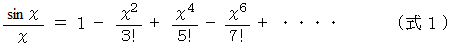
この式の左辺は、
 が次のような値を取るときに 0 になります。
が次のような値を取るときに 0 になります。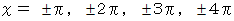

したがって、
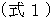 の左辺は次のように書けるはずです。
の左辺は次のように書けるはずです。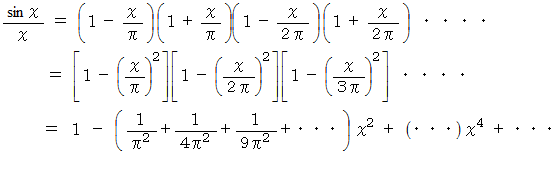
この式 と
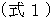 の右辺の
の右辺の 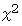 の項は等しいので、 次の式が成り立ちます、
の項は等しいので、 次の式が成り立ちます、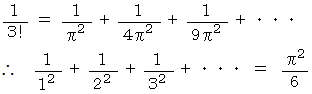
では、 次の式はいくらになると思いますか?
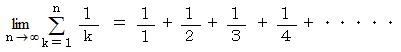
答えは、 無限大です。 次のようにして答えを導くことができます。
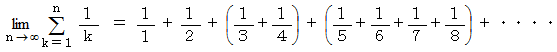
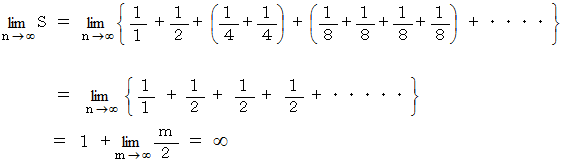
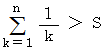 であるから
であるから 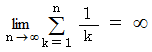 である。
である。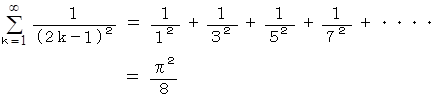
( 証明 )
-
マクローリン展開 :
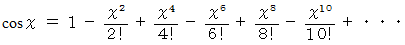
この式の左辺は、 x が次のような値を取るときに 0 になります。
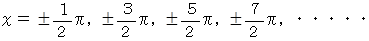
したがって、 cos x は次のように書くことができます
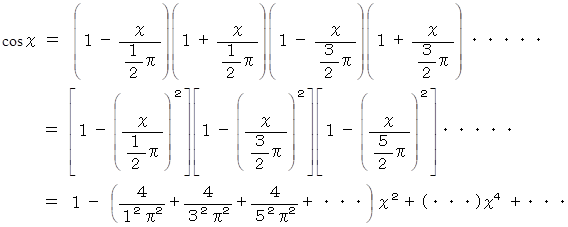
この式とマクローリン展開式の x2 の係数を比べると、
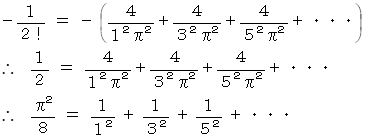
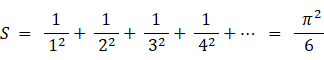
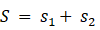
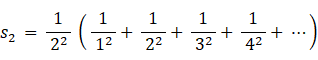
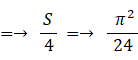
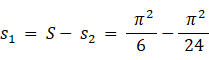
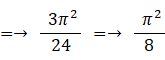
 数理論 へ戻る
数理論 へ戻る