(1) 実数の場合

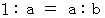
よって

よって
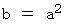

よって

よって
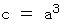
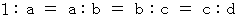
よって
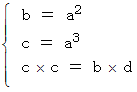
よって
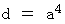
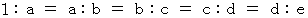
よって

よって
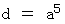
こうして、
数列 :
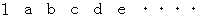 は、
は、数列 :
 であり、
であり、それは、 初項
 、 公比
、 公比  の等比数列であることがわかりました。
の等比数列であることがわかりました。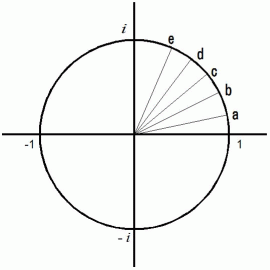
円周上の点
 と 原点を結ぶ直線が 実数軸 ( 横軸 ) と交わる角度を
と 原点を結ぶ直線が 実数軸 ( 横軸 ) と交わる角度を  とし、
とし、それから同じ角度だけ反時計回りに離れた円周上の点を
 とし、 それから ・ ・ ・
とし、 それから ・ ・ ・

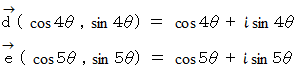
 これらのベクトルの大きさはすべて
これらのベクトルの大きさはすべて  です。
です。
よって
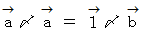
よって
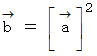
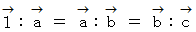
よって
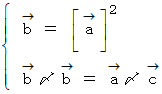
よって

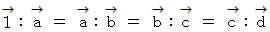
よって
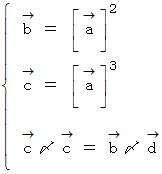
よって
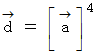
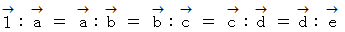
よって

よって
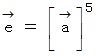
こうして、
数列 :
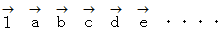 は、
は、数列 :
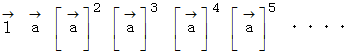 であり、
であり、それは、 初項
 、 公比
、 公比 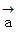 の等比数列であることがわかりました。
の等比数列であることがわかりました。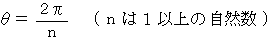 のとき
のとき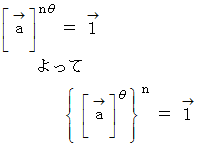
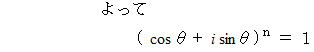

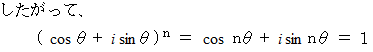
これは、 「 ド・モアブルの定理 」 の証明になっています。 また、 以上の考察は、 次のような
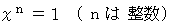 の解を求めるのにも応用されます。
の解を求めるのにも応用されます。
( 答 え )
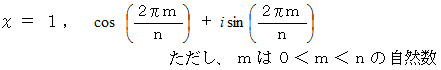
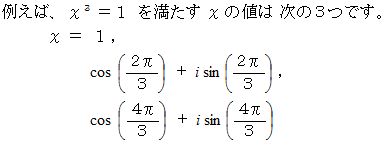
最後に、 次の式が成り立っていることを確かめておきましょう。

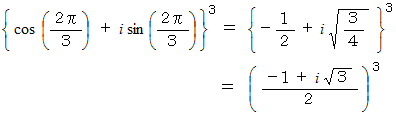

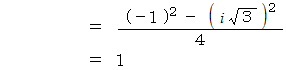
 数理論 へ戻る
数理論 へ戻る